월간 코드 챌린지 시즌2 > 2개 이하로 다른 비트
문제 설명
양의 정수 x에 대한 함수 f(x)를 다음과 같이 정의합니다.
x보다 크고 x와 비트가 1~2개 다른 수들 중에서 제일 작은 수
시각화
2가 주어졌을 때 비트 차이가 1 ~ 2 개 다른 수 중에서 제일 작은 수는 3이다.
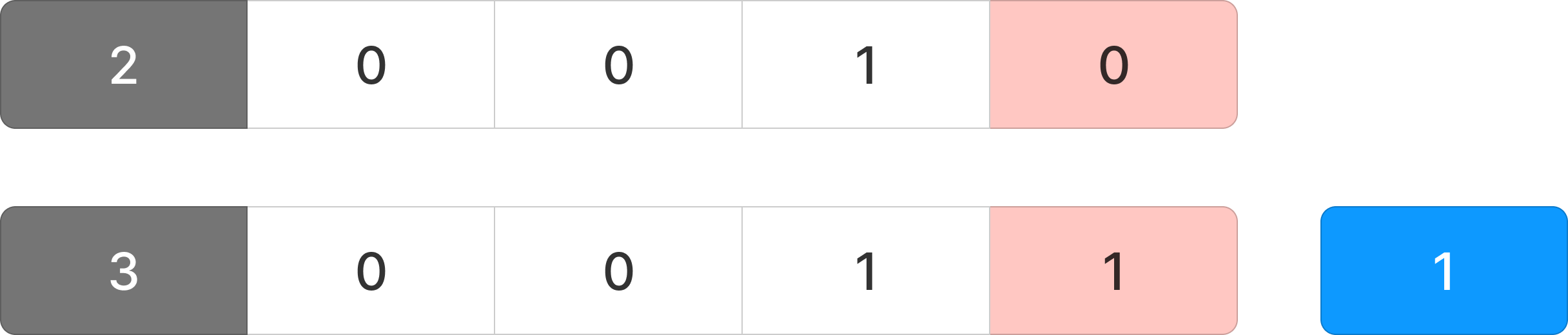
7이 주어졌을 때 비트 차이가 1 ~ 2 개 다른 수 중에서 제일 작은 수는 11이다.

문제 해결 과정
사실 문제를 풀 때 처음 시도한 것은 1씩 증가시키며 ^ 연산자를 사용해서 1 ~ 2 개 다른 비트를 찾아내는 것이었다. 너무 당연하게도 시간 초과가 발생하였다. 왜 자꾸 손이 가는지 모르겠다.
63231 이 주어졌을 때를 보면 1을 증가시키면 달라지게 되는 비트가 많은 것을 볼 수 있다. 이 수는 너무 길어지면 그림이 너무 작게 보여 적당한 수를 가져왔을 뿐 훨씬 더 차이가 많이 나는 수가 있다. 그러기에 ^ 연산자를 사용해서 1 ~ 2 개 다른 비트를 찾아내는 것은 굉장히 비효율적이다.

그렇다면 어떻게 효율적으로 계산을 할 수 있을까에 대해 고민하다가 규칙을 발견했다.
규칙 기반 풀이
주어진 수의 2진수의 맨 뒤 비트 0 과 1일 때 규칙을 찾아보면 아래와 같다.
0 일 때
주어진 수 + 1
1 일 때
맨 뒤에서부터 0을 찾고 1로 바꾼 후 그 다음 비트를 0으로 바꾼다.
0일 때는 너무 간단하니 생략하고 1일 때 도식화를 해보자.

문자열이 배열이 아니라 바로 위치를 바꾸지 못하니 slice 을 사용해서 처리하도록 하였다.

문제를 풀고 다른 사람 풀이를 보니 비트 연산자로만 풀 수 있는데 아직 그 방법이 왜 가능한지 모르겠어 이 글에 적지는 않겠다.
비트 연산 풀이
63231 과 63232 를 XOR 하면 아래와 같이 1이 연속적으로 나오게 된다. 우리가 규칙 기반 풀이에서 보았듯 0 과 1 의 자리를 바꾸면 되는 것이다.

아래 그림에서 첫 번 째 표는 XOR 을 한 값이다. 1일 경우 다른 비트를 의미한다. 여기서 시프트 연산자로 2만큼 이동하게 되면 뒤에 1이 2개가 사라진다.

이러한 방법으로 기존 값인 63231 에서 (63231 ^ 63232) » 2 를 한 값을 더한다. 즉 63231 + (63231 ^ 63232) » 2 를 하는 것이다.
이렇게 하면 맨 뒤 연산자가 0인 것을 알 수 있다. 그렇기에 +1 을 추가적으로 해주면 된다.

만약 a ^ b 를 했을 때 규칙 기반처럼 맨 뒤의 비트만 달라진 경우에는 000001 이런 식이기에 시프트 연산자 2번하면 0이 된다. 그렇기에 +1 을 해주면 된다. 즉 규칙 기반 풀이를 통해 비트 연산자 조합으로 풀 수 있다.

전체 코드
규칙 기반 풀이
def solution(numbers):
answer = []
for number in numbers:
a_b = '0' + format(number, 'b')
if a_b[-1] == '0':
answer.append(number + 1)
continue
for i in range(len(a_b) - 1, -1, -1):
if a_b[i] == '0':
answer.append(int((a_b[0:i] + '1' + '0' + a_b[i + 2:]), 2))
break
return answer
print(solution([2, 7]), [3, 11])
print(solution([1]), [2])
solution([10 ** 15 - i * 5 for i in range(100000)]) # 오래 걸리면 시간 초과 발생
비트 연산 풀이
def solution(numbers):
return [n + ((n ^ n + 1) >> 2) + 1 for n in numbers]