맬서스 모델과 로지스틱 함수
결론
맬서스 모델은 상승의 끝이 한계가 없지만 로지스틱 함수는 상승의 끝이 한계가 있다.
맬서스 모델
맬서스의 저서 『인구론』 에서 이 속도가 해당 시점에 존재하는 개체 수에 비례한다고 가정하고 아래와 같은 모델을 제시했다.
(개체 수가 증가하는 속도) $ = rN $
r 은 개체가 증식하는 속도
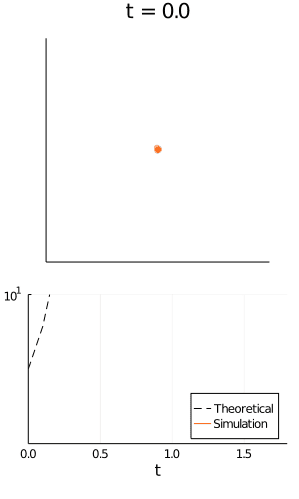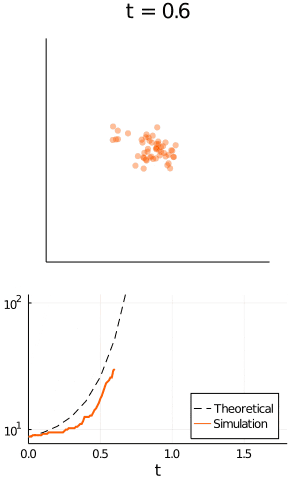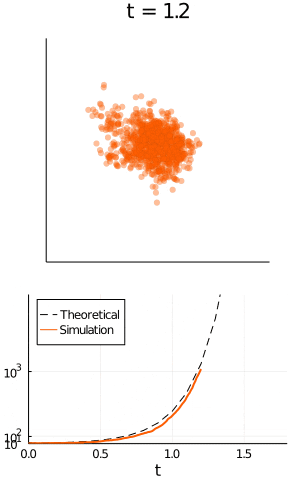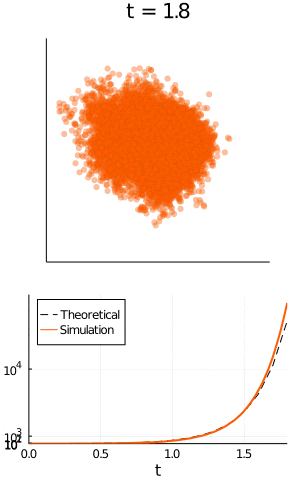
$N(t)=N_0e^{rt} $
맬서스 모델의 한계
조금 더 생각해보면 생물의 번식은 자원이 유한하기 때문에 어느 정도까지는 증가하지만 어느 정도 이상이 되면 자원이 부족해져서 증식이 멈추게 된다. 즉 너무 늘어나면 다시 줄어들게 된다.
로지스틱 함수
로지스틱 함수는 환경 수용 능력을 나타내는 매개변수가 추가되었다.
$\frac{dt}{dN}=r(1-\frac{K}{N})$
해
$N(t)=\frac{K-N_0+N_0e^{rt}}{N_0Ke^{rt}}$
효모(Saccharomyces cerevisiae)의 개체 수 변동
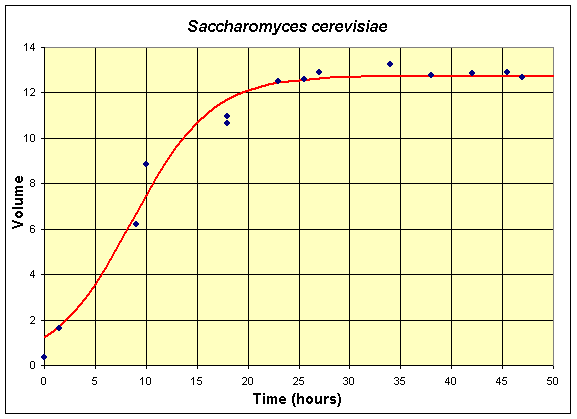
1번째 이미지 출처: https://freshrimpsushi.github.io/posts/malthusian-growth-model/
2번째 이미지 출처: https://jmahaffy.sdsu.edu/courses/f00/math122/lectures/competition/competition.html/
정보 출처 : 에자키 타카히로. 『데이터 분석을 위한 수리 모델 입문』
