2019 KAKAO BLIND RECRUITMENT 후보키
문제 설명
프렌즈대학교 컴퓨터공학과 조교인 제이지는 네오 학과장님의 지시로, 학생들의 인적사항을 정리하는 업무를 담당하게 되었다.
그의 학부 시절 프로그래밍 경험을 되살려, 모든 인적사항을 데이터베이스에 넣기로 하였고, 이를 위해 정리를 하던 중에 후보키(Candidate Key)에 대한 고민이 필요하게 되었다.
후보키에 대한 내용이 잘 기억나지 않던 제이지는, 정확한 내용을 파악하기 위해 데이터베이스 관련 서적을 확인하여 아래와 같은 내용을 확인하였다.
관계 데이터베이스에서 릴레이션(Relation)의 튜플(Tuple)을 유일하게 식별할 수 있는 속성(Attribute) 또는 속성의 집합 중, 다음 두 성질을 만족하는 것을 후보 키(Candidate Key)라고 한다.
유일성(uniqueness) : 릴레이션에 있는 모든 튜플에 대해 유일하게 식별되어야 한다.
최소성(minimality) : 유일성을 가진 키를 구성하는 속성(Attribute) 중 하나라도 제외하는 경우 유일성이 깨지는 것을 의미한다. 즉, 릴레이션의 모든 튜플을 유일하게 식별하는 데 꼭 필요한 속성들로만 구성되어야 한다.
제이지를 위해, 아래와 같은 학생들의 인적사항이 주어졌을 때, 후보 키의 최대 개수를 구하라.
시각화
아래와 같이 학생들의 인적사항이 주어졌을 때 후보키의 최대 개수를 구해야 한다.
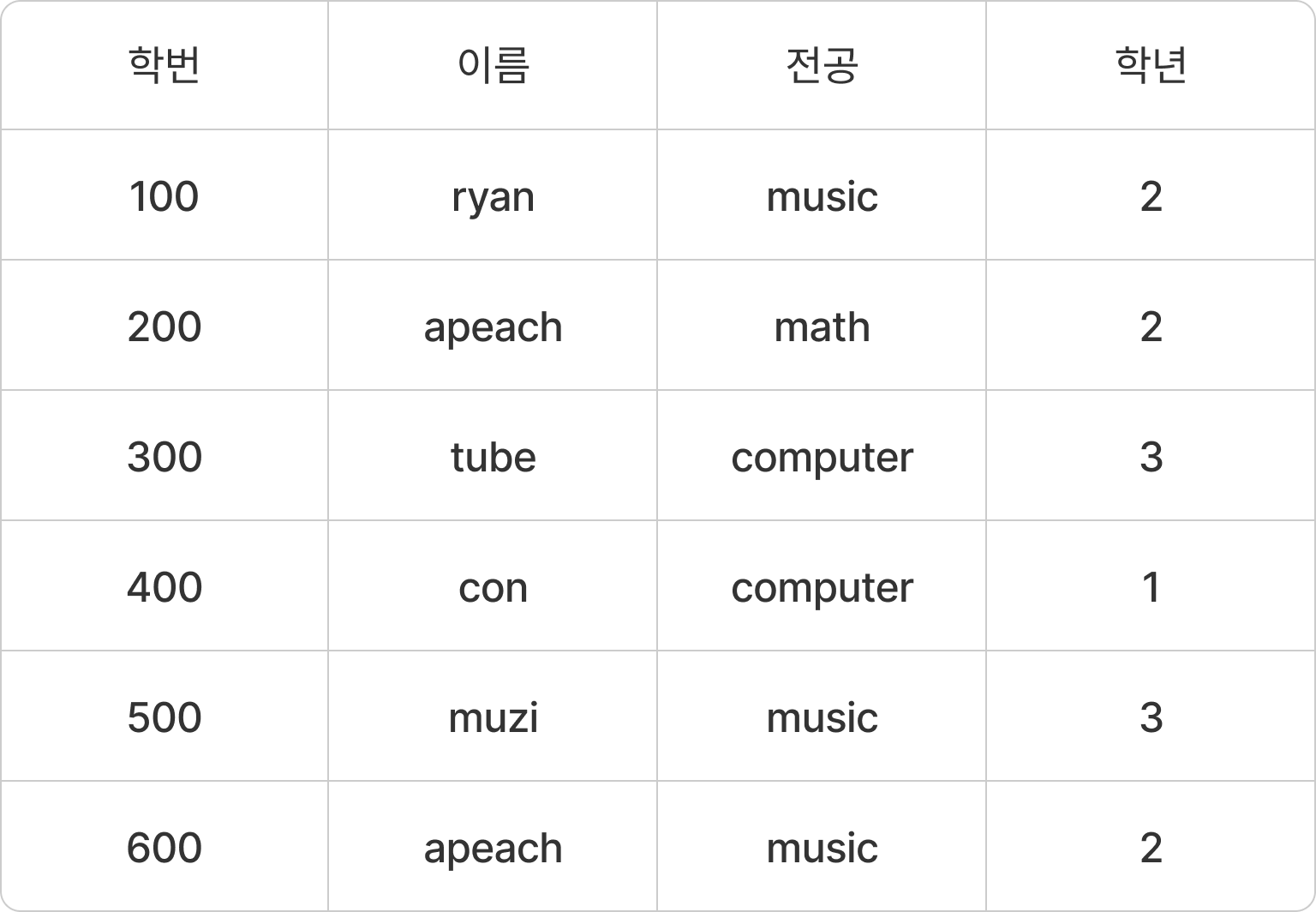
학번을 키로 사용할 경우 유일성과 최소성을 만족한다. 이유는 학번이 겹치는 경우가 없기에 유일성이 만족되며 학번 단 하나의 컬럼으로 식별할 수 있기 때문에 최소성을 만족한다.

이름을 키로 사용할 경우 유일성이 만족하지 않는다. apeach 가 겹치는 것을 확인할 수 있다.
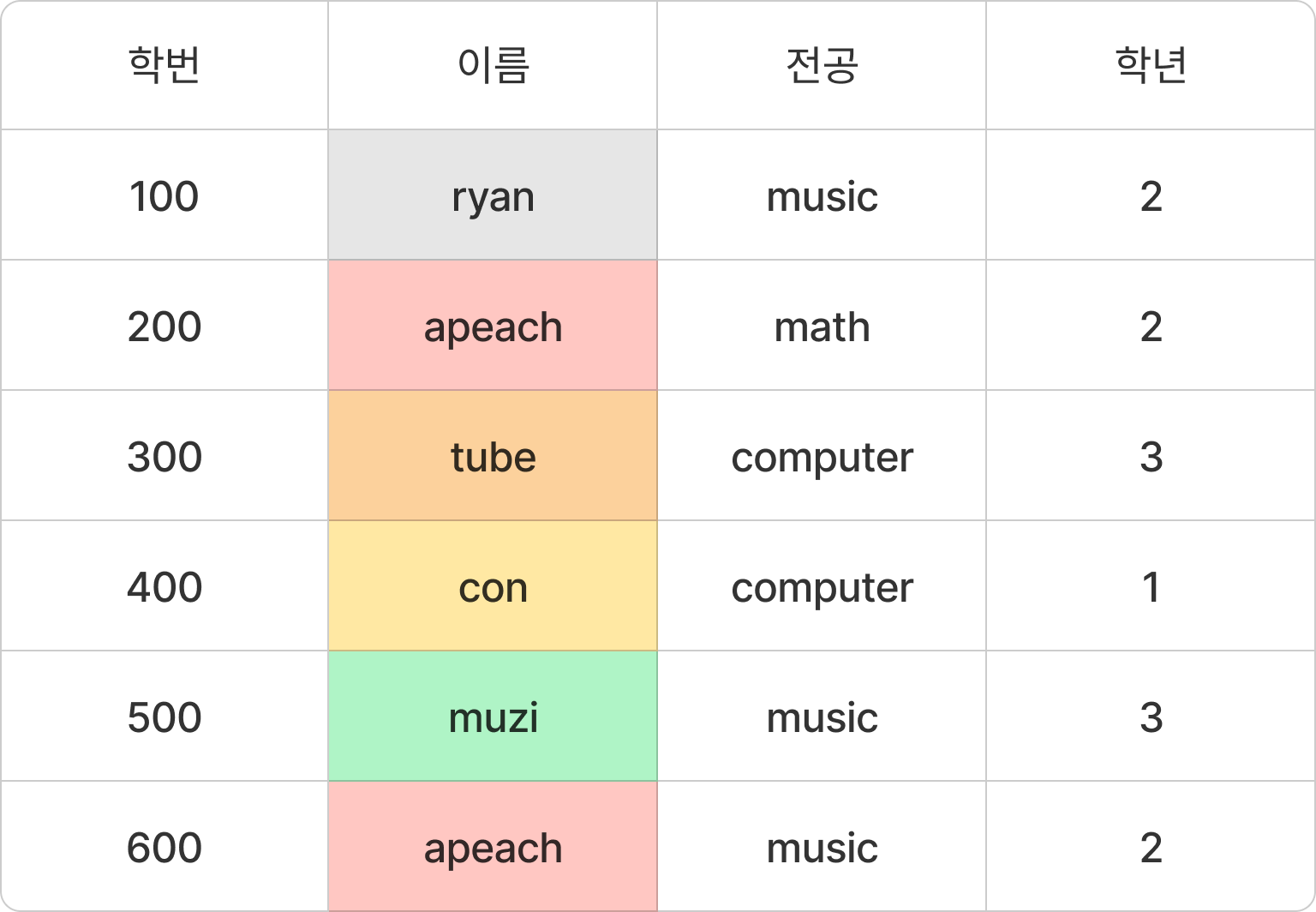
전공을 키로 사용할 경우 유일성이 만족하지 않는다. computer 가 겹치는 것을 확인할 수 있다.

만약 이름과 전공을 함께 키로 사용할 경우 유일성과 최소성을 만족한다.

이와 같이 후보키를 찾아내는 것이 문제의 핵심이다.
최소성을 만족한다는 것은 어떻게 알 수 있을까?
아래는 최소성을 만족하지 않는 경우이다. 이유는 학번 자체로 유일성을 만족하기 때문에 학번과 이름 조합은 최소성을 위반하는 것이다.

그렇다면 작은 경우부터 시작해서 최대 경우까지 찾아내면 된다. 단 유일성을 만족할 경우 최소성을 만족하는지 확인해야 한다.
이를 달리 달하면 기존 후보키가 현재 후보키의 부분집합인지 확인하면 된다.
문제 해결 과정
모든 경우의 수를 확인해야하기 때문에 조합을 사용해야 한다.
모든 경우의 수를 확인하기 위해 조합을 사용
예제처럼 4개의 컬럼이 있다고 한다면 아래와 같은 경우의 수가 나온다.
- (0)
- (1)
- (2)
- (3)
- (0, 1)
- (0, 2)
- (0, 3)
- (1, 2)
- (1, 3)
- (2, 3)
- (0, 1, 2)
- (0, 1, 3)
- (0, 2, 3)
- (1, 2, 3)
- (0, 1, 2, 3)
위처럼 만들기 위해서는 아래와 같은 코드를 작성하면 된다.
from itertools import combinations
result = []
columns = [i for i in range(len(relation[0]))] # 열 인덱스 생성
for i in range(1, len(columns) + 1): # 조합 크기를 1부터 열의 개수까지 반복
for comb in combinations(columns, i): # 해당 크기의 조합 생성
result.append(comb)
# result에는 모든 조합이 저장됨
Comprehension 을 사용하면 아래와 같이 작성할 수 있다.
[comb for i in range(1, len(relation[0]) + 1) for comb in combinations([i for i in range(len(relation[0]))], i)]
최소성을 만족
집합 자료구조인 set 을 사용하면 부분집합을 확인할 수 있다. issuperset 을 사용해서 집합 관계를 확인하면 된다.
def is_subset_of_existing(candidate, existing_key):
return any([set(candidate).issuperset(key) for key in existing_key])
위 2개만 가지면 이 문제를 해결할 수 있다.
전체 코드
from itertools import combinations
def solution(relation):
def is_subset_of_existing(candidate, existing_key):
return any([set(candidate).issuperset(key) for key in existing_key])
candidate_list = []
for comb in [comb for i in range(1, len(relation[0]) + 1) for comb in
combinations([i for i in range(len(relation[0]))], i)]:
if is_subset_of_existing(comb, candidate_list):
continue
if len(relation) == len(set([','.join([str(rel[c]) for c in comb]) for rel in relation])):
candidate_list.append(list(comb))
return len(candidate_list)