깊이/너비 우선 탐색(DFS/BFS) > 타겟 넘버
문제 설명
n개의 음이 아닌 정수들이 있습니다. 이 정수들을 순서를 바꾸지 않고 적절히 더하거나 빼서 타겟 넘버를 만들려고 합니다. 예를 들어 [1, 1, 1, 1, 1]로 숫자 3을 만들려면 다음 다섯 방법을 쓸 수 있습니다.
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
사용할 수 있는 숫자가 담긴 배열 numbers, 타겟 넘버 target이 매개변수로 주어질 때 숫자를 적절히 더하고 빼서 타겟 넘버를 만드는 방법의 수를 return 하도록 solution 함수를 작성해주세요.
시각화
문제 예시에서는 [1, 1, 1, 1, 1] 로 주어졌지만 이를 시각화하기에는 경우의 수가 많아서 [1, 2, 3] 으로 시각화 해보려한다.
[1, 2, 3] 이 주어질 때 우리는 아래와 같은 경우의 수를 구해야한다. 그래야 합한 값이 target 과 같은지 확인할 수 있기 때문이다.
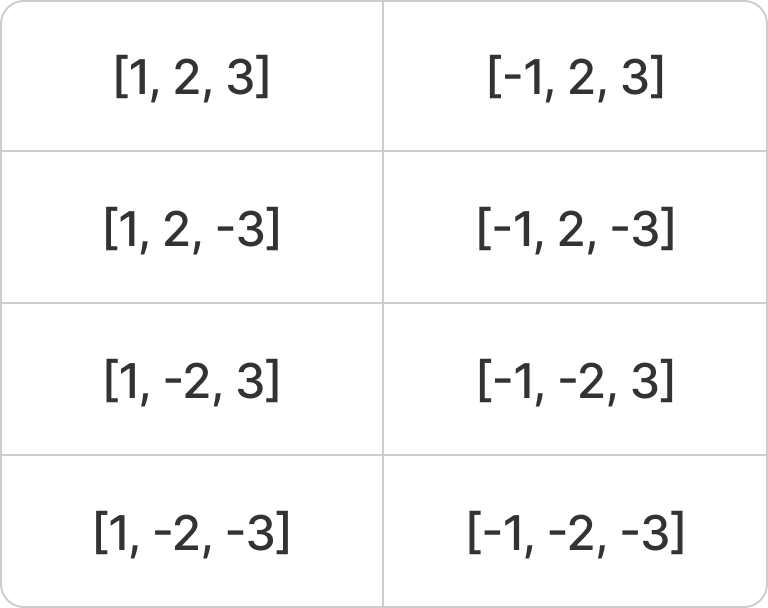
문제 해결 과정
이 문제의 경우 같은 결이지만 다르게 2가지 방법으로 풀 수 있다.
BFS 로 풀기
시각화에 나온 그림처럼 경우의 수를 만들려면 BFS 딱 떠오르는 방법이다. 아래와 같이 하나씩 요소를 +, - 로 추가하며 경우의 수를 만들어 나가면 된다.

데카르트 곱으로 풀기
데카르트 곱(Cartesian Product)이란 두 집합의 모든 원소 쌍을 조합하여 새로운 집합을 생성하는 연산을 말한다. 이 문제에서 데카르트 곱이 적절한 이유는 데카르트 곱은 순서를 고려한다.
집합 A = {1, 2} , B = {x, y, z} 가 있을 때:
$ A \times B $ = {(1, x), (1, y), (1, z), (2, x), (2, y), (2, z)}
python 에서는 itertools.product 를 사용하면 데카르트 곱을 구할 수 있다.
전체 코드
BFS 로 풀기
import collections
def solution(numbers, target):
def bfs():
q = collections.deque([[numbers[0]], [-numbers[0]]])
possible = []
while q:
arr = q.popleft()
if len(arr) == len(numbers):
print(arr)
if sum(arr) == target:
possible.append(arr)
continue
q.append(arr + [numbers[len(arr)]])
q.append(arr + [-numbers[len(arr)]])
return possible
return len(bfs())

데카르트 곱으로 풀기
from itertools import product
def solution(numbers, target):
return list(map(sum, product(*[(num, -num) for num in numbers]))).count(target)
같은 논리라고는 하지만 데카르트 곱으로 푸는 것이 더 간결하고 빠르다.
