2025 프로그래머스 코드챌린지 1차 예선 > Lv2. 지게차와 크레인
문제 설명
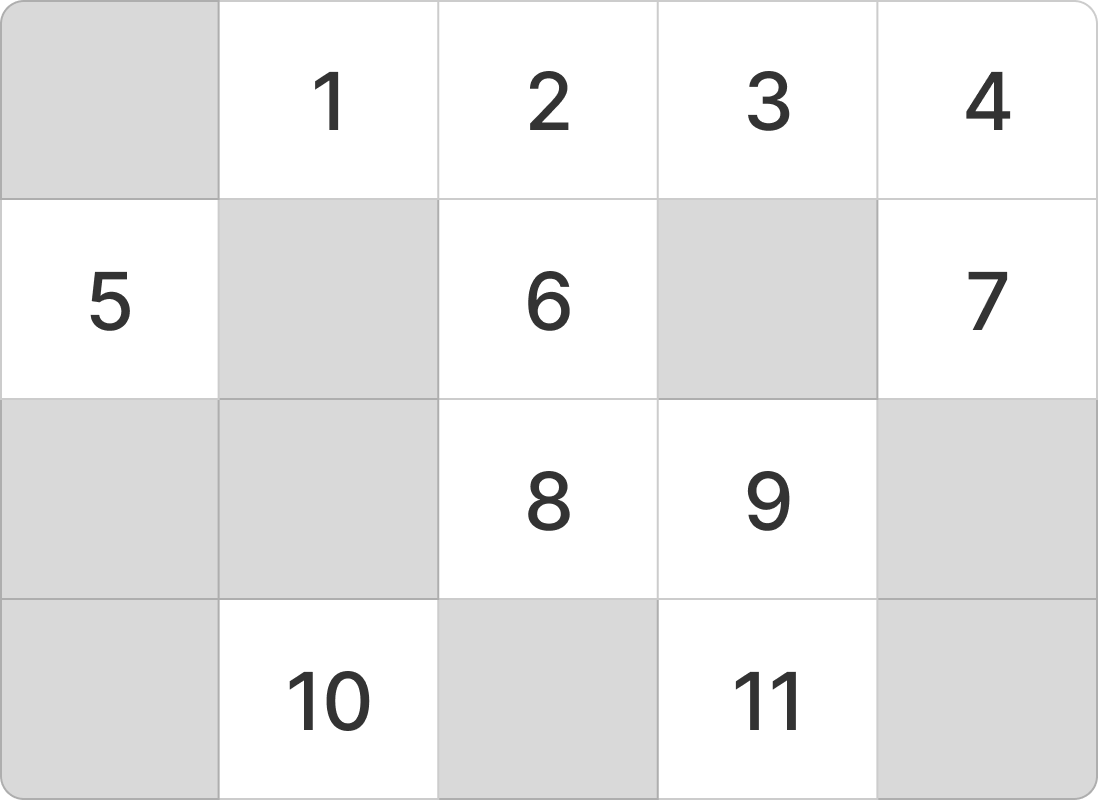
A 회사의 물류창고에는 알파벳 대문자로 종류를 구분하는 컨테이너가 세로로 n 줄, 가로로 m줄 총 n x m개 놓여 있습니다. 특정 종류 컨테이너의 출고 요청이 들어올 때마다 지게차로 창고에서 접근이 가능한 해당 종류의 컨테이너를 모두 꺼냅니다. 접근이 가능한 컨테이너란 4면 중 적어도 1면이 창고 외부와 연결된 컨테이너를 말합니다.
최근 이 물류 창고에서 창고 외부와 연결되지 않은 컨테이너도 꺼낼 수 있도록 크레인을 도입했습니다. 크레인을 사용하면 요청된 종류의 모든 컨테이너를 꺼냅니다.
시각화
하나의 케이스를 시각화하면 아래와 같다.

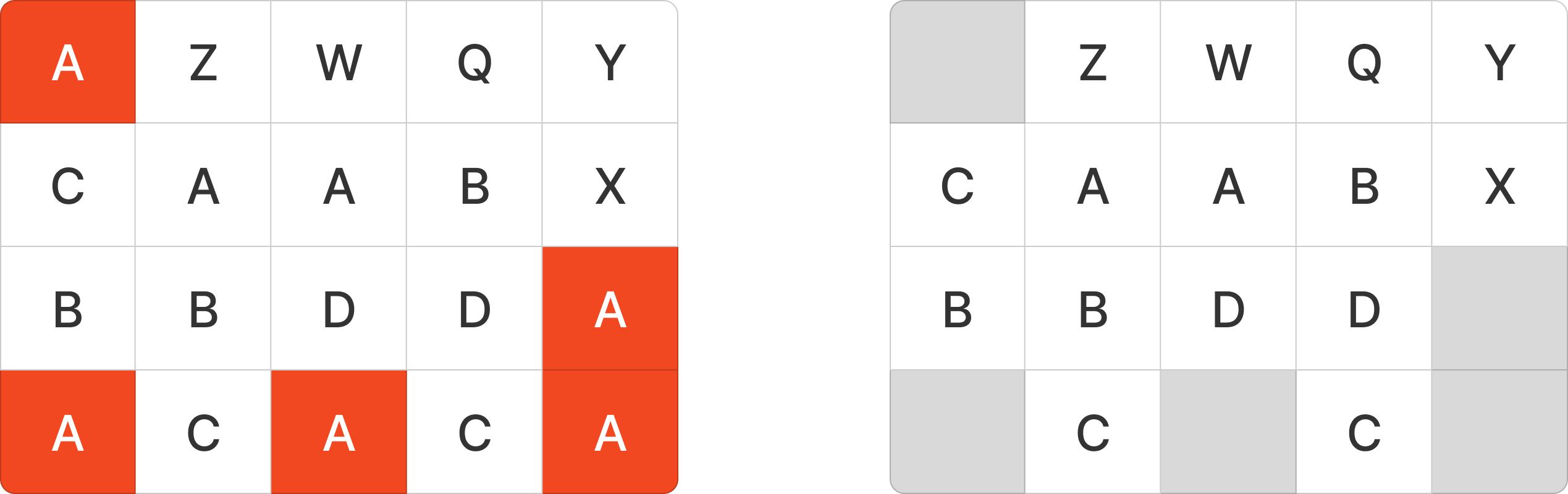
A 를 지게차로 꺼낸다면 아래와 같이 뺄 수 있다. 지게차로 가져올 때는 외부에서 접근할 수 있는 컨테이너만 가져올 수 있다.
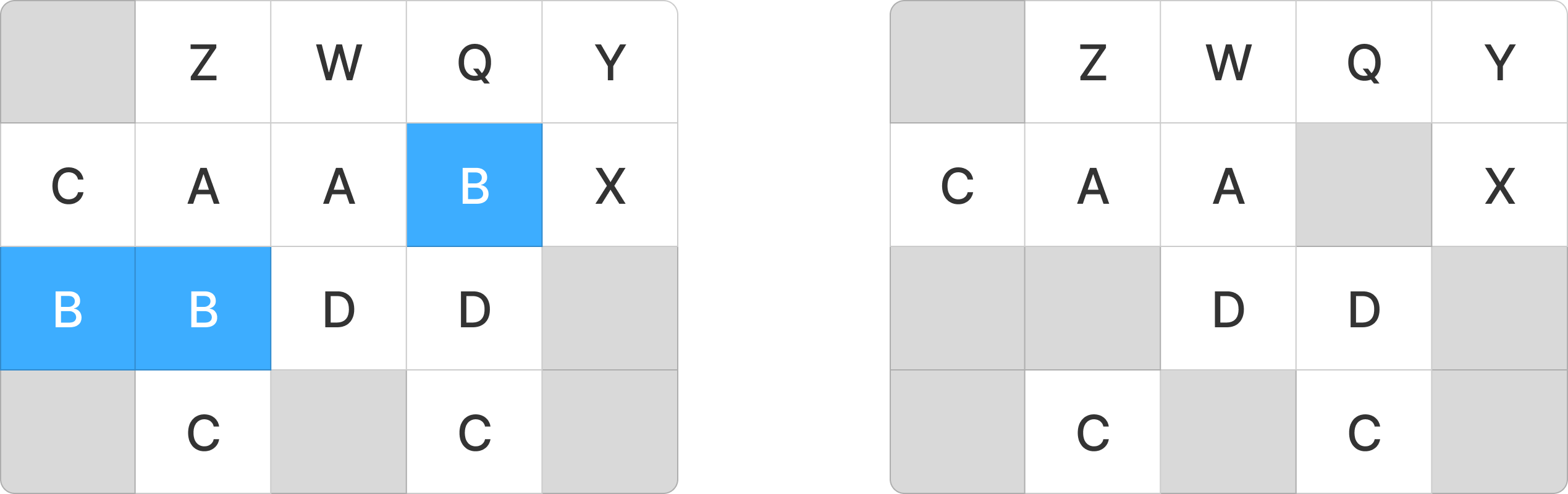
B 를 크레인으로 꺼낸 경우는 아래와 같다. 크레인은 창고 내부에 있는 컨테이너를 모두 꺼낼 수 있다.
즉 크레인을 사용하면 모든 컨테이너를 꺼낼 수 있다.
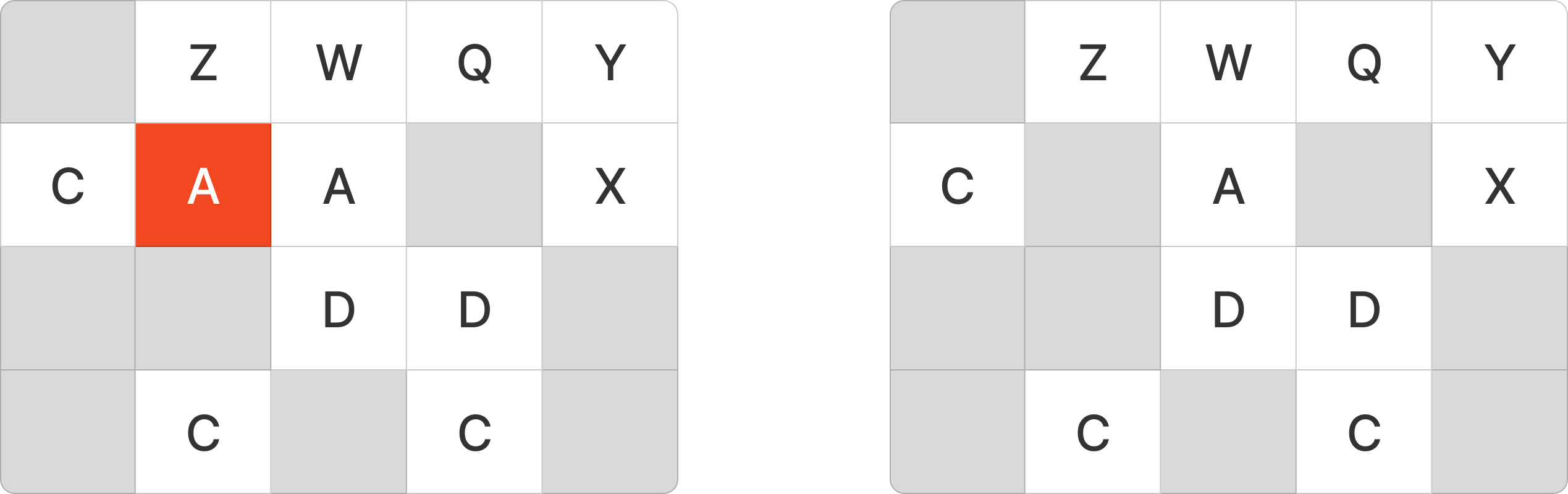
다시 A 를 지게차로 꺼내는 경우는 아래와 같다. A 두 개가 붙어있지만 외부에서 접근할 수 있는 것은 하나뿐이다.
이러한 방식으로 컨테이너를 꺼내고 남은 컨테이너의 개수를 구하는 문제이다.
문제 해결 과정
간단하게 코드를 작성하고 싶었지만 그리고 그럴려고 했지만 코드가 길어져 아쉰 마음이 가득하다.
그렇지만 코드 자체보다는 접근법을 설명하고자 한다.
우선 첫 번째로 고민했던 것은 지게차로 가져갈 수 있는 컨테이너를 가지고 있을지 또는 지게차로 가져갈 수 있는 컨테이너 외부 영역 좌표 값을 저장해야 할지에 대한 것이었다. 이 고민에 대해서는 지게차로 가져갈 수 있는 컨테이너를 저장하는 것이 더 효율적이라고 판단했다. 이유는 컨테이너 외부 영역 좌표를 가지고 있다면 모든 컨테이너를 돌며 매번 상하좌우를 확인해야하기 때문이다. 이로 인해 더 비효율적일 것이라고 판단했다.
이제 시각화를 통해 어떻게 풀었는지 보자.
컨테이너 외부 영역 추가
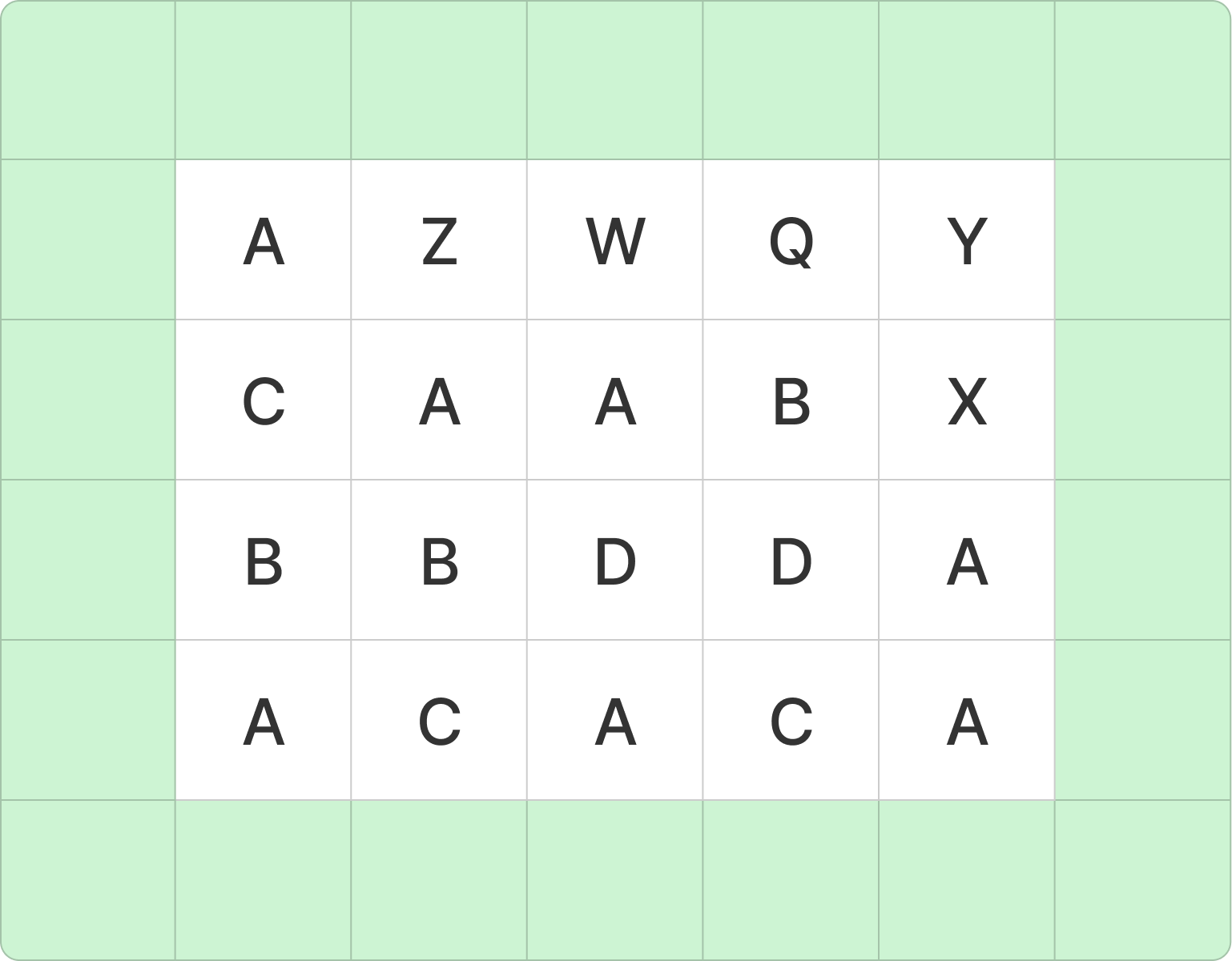
연한 초록색으로 컨테이너를 감싸도록 하였다. 연한 초록색의 역할은 컨테이너 상하좌우에 연한 초록색이 있다면 지게차로 가져갈 수 있는 컨테이너라는 것을 의미한다.
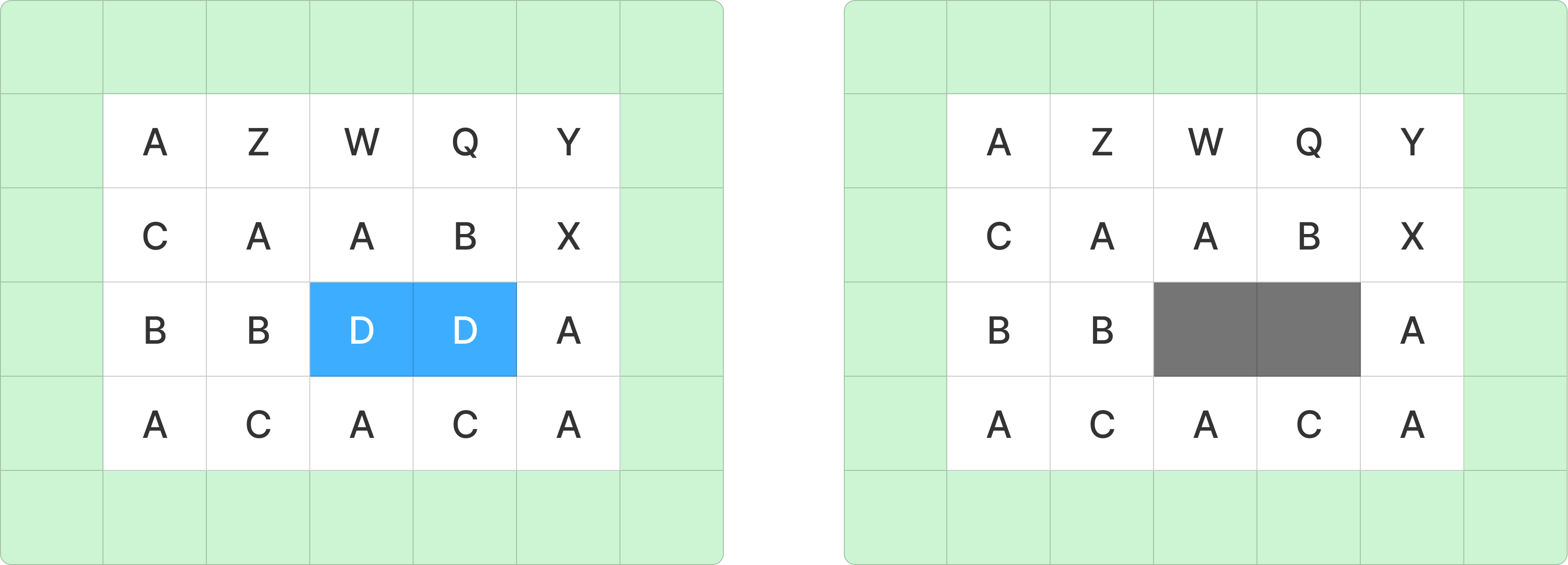
왜 연한 초록색이 필요할까? 아래와 같이 D 가 크레인으로 뽑혀갈 때 컨테이너 안에 감싸져 외부 영역에서 접근할 수 없는 영역이 되었다.
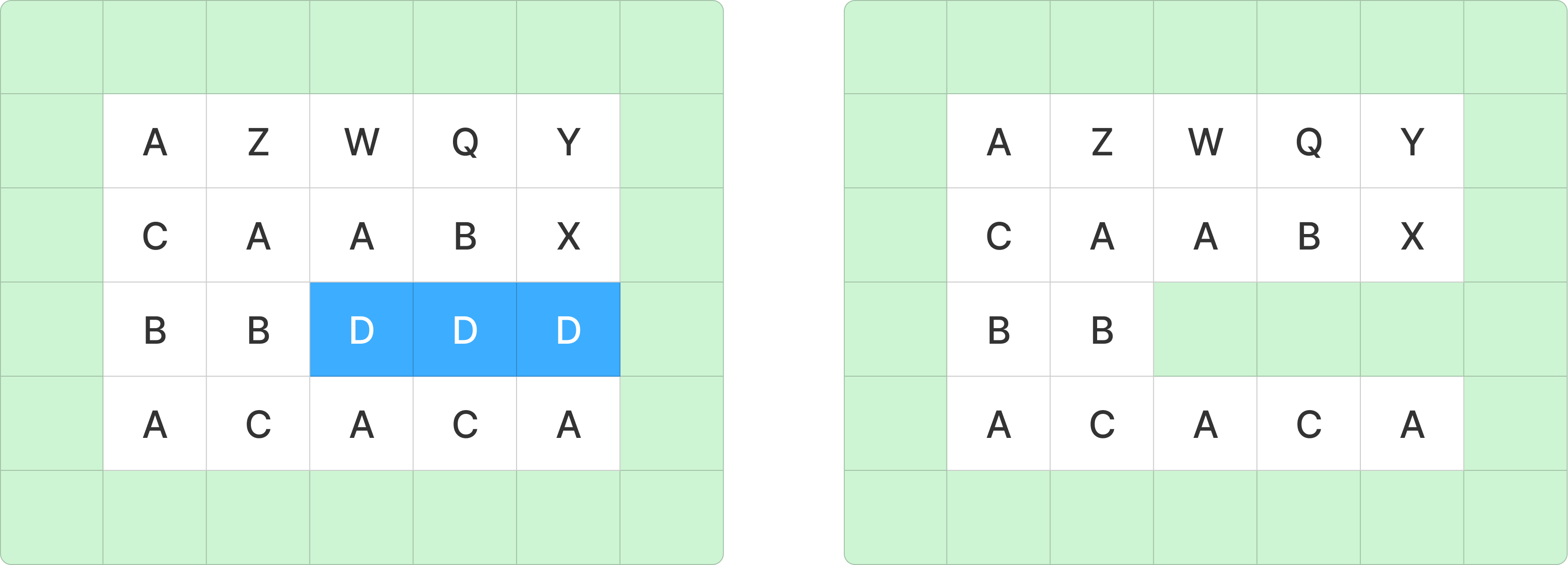
크레인으로 제거할 때 연한 초록색과 닿아있는 부분이 있다면 지게차로 가져갈 수 있는 영역이 생긴 것이라는 것을 의미한다.
작업 요청에 따른 컨테이너 제거
A
진한 초록색은 지게차로 가져갈 수 있는 컨테이너를 의미한다. A 를 지게차로 가져갈 때는 아래와 같이 지게차로 가져갈 수 있는 컨테이너를 모두 제거한다. 그 후 연결 가능한 연한 초록색이 있다면 지게차로 가져갈 수 있는 컨테이너를 추가한다.

BB
BB 를 크레인으로 제거할 때는 아래와 같이 모두 제거한다. 왼쪽에 BB 는 2개가 붙어있고 외부와 연결이 가능하기에 연한 초록색 영역으로 처리해야한다.

A
A 를 다시 지게차로 가져가면 아래 그림과 같이 하나만 가져갈 수 있다. 오른쪽에 있는 A 는 갇혀있기 때문이다.

전체 코드
위 내용을 코드로 구현하면 아래와 같다.
참고하고 싶다면 코드 자체보다는 위에 시각화한 그림을 참고하길 바란다.
from collections import defaultdict, deque
def solution(storage, requests):
def is_valid_yx(y, x):
return 0 <= y < len(storage) or 0 <= x < len(storage[0])
answer = len(storage) * len(storage[0])
for y in range(len(storage)):
storage[y] = [''] + [a for a in storage[y]] + ['']
storage.insert(0, ['' for _ in storage[0]])
storage.append(['' for _ in storage[0]])
available_storages = defaultdict(set)
for y in range(len(storage)):
for x in range(len(storage[0])):
if not ((y == (0 + 1) or y == len(storage) - 1 - 1) or (x == 0 + 1 or x == len(storage[0]) - 1 - 1)):
continue
available_storages[storage[y][x]].add((y, x))
for req in requests:
def explore_available_storage(yx):
y, x = yx[0], yx[1]
is_able = False
explore_yx = {(y, x)}
pop_yx = {(y, x)}
possible_yx, visit_yx = set(), set()
while explore_yx:
ey1, ex1 = explore_yx.pop()
for py1, px1 in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
y2, x2 = ey1 + py1, ex1 + px1
if not is_valid_yx(y2, x2) or (y2, x2) in visit_yx:
continue
if storage[y2][x2] == '':
is_able = True
if storage[y2][x2] == 'POP':
explore_yx.add((y2, x2))
pop_yx.add((y2, x2))
if len(req) == 1:
storage[y2][x2] = ''
else:
possible_yx.add((y2, x2))
if len(req) == 1:
available_storages[storage[y2][x2]].add((y2, x2))
visit_yx.add((y2, x2))
if is_able:
for yx in pop_yx:
storage[yx[0]][yx[1]] = ''
for yx in possible_yx:
available_storages[storage[yx[0]][yx[1]]].add((yx[0], yx[1]))
if len(req) == 1:
if req not in available_storages:
continue
containers_yx = available_storages[req]
for yx in containers_yx.copy():
y1, x1 = yx
if storage[y1][x1] == '':
continue
answer -= 1
storage[y1][x1] = ''
explore_available_storage((y1, x1))
else:
for y in range(len(storage)):
for x in range(len(storage[0])):
if storage[y][x] != req[0]:
continue
answer -= 1
storage[y][x] = 'POP'
explore_available_storage((y, x))
return answer