이분탐색 > 입국심사
문제 설명
n명이 입국심사를 위해 줄을 서서 기다리고 있습니다. 각 입국심사대에 있는 심사관마다 심사하는데 걸리는 시간은 다릅니다.
처음에 모든 심사대는 비어있습니다. 한 심사대에서는 동시에 한 명만 심사를 할 수 있습니다. 가장 앞에 서 있는 사람은 비어 있는 심사대로 가서 심사를 받을 수 있습니다. 하지만 더 빨리 끝나는 심사대가 있으면 기다렸다가 그곳으로 가서 심사를 받을 수도 있습니다.
모든 사람이 심사를 받는데 걸리는 시간을 최소로 하고 싶습니다.
입국심사를 기다리는 사람 수 n, 각 심사관이 한 명을 심사하는데 걸리는 시간이 담긴 배열 times가 매개변수로 주어질 때, 모든 사람이 심사를 받는데 걸리는 시간의 최솟값을 return 하도록 solution 함수를 작성해주세요.
제한사항
- 입국심사를 기다리는 사람은 1명 이상 1,000,000,000명 이하입니다.
- 각 심사관이 한 명을 심사하는데 걸리는 시간은 1분 이상 1,000,000,000분 이하입니다.
- 심사관은 1명 이상 100,000명 이하입니다.
시각화
n 이 6이라는 것은 6명이 입국심사를 받아야 한다는 것이다.
times 가 [7, 10] 이라는 것은 각 심사관이 7분, 10분이 걸린다는 것이다.
이 때 6명을 처리할 때 아래와 같이 처리하여 28분이 소요된다.
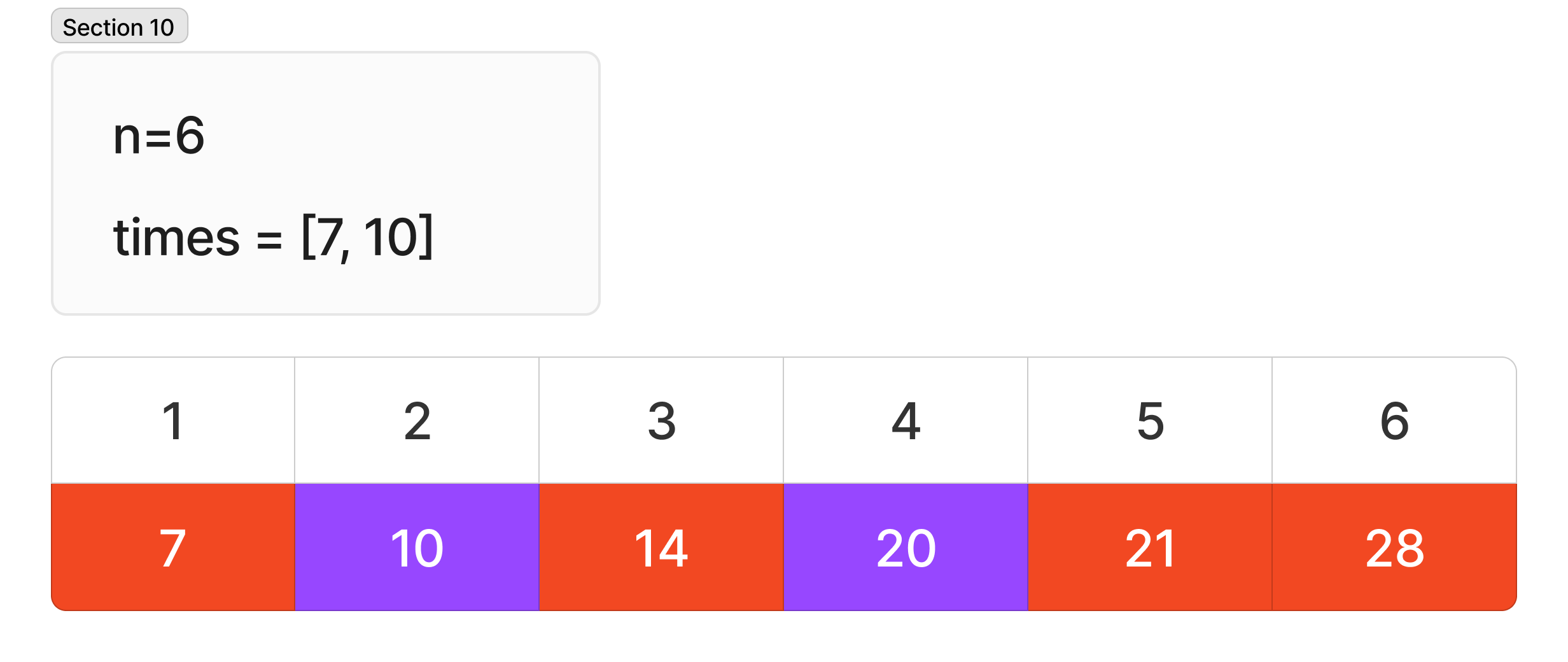
n 이 6 이면서 times 가 [7, 10, 10] 경우는 아래와 같이 20분이 소요된다.
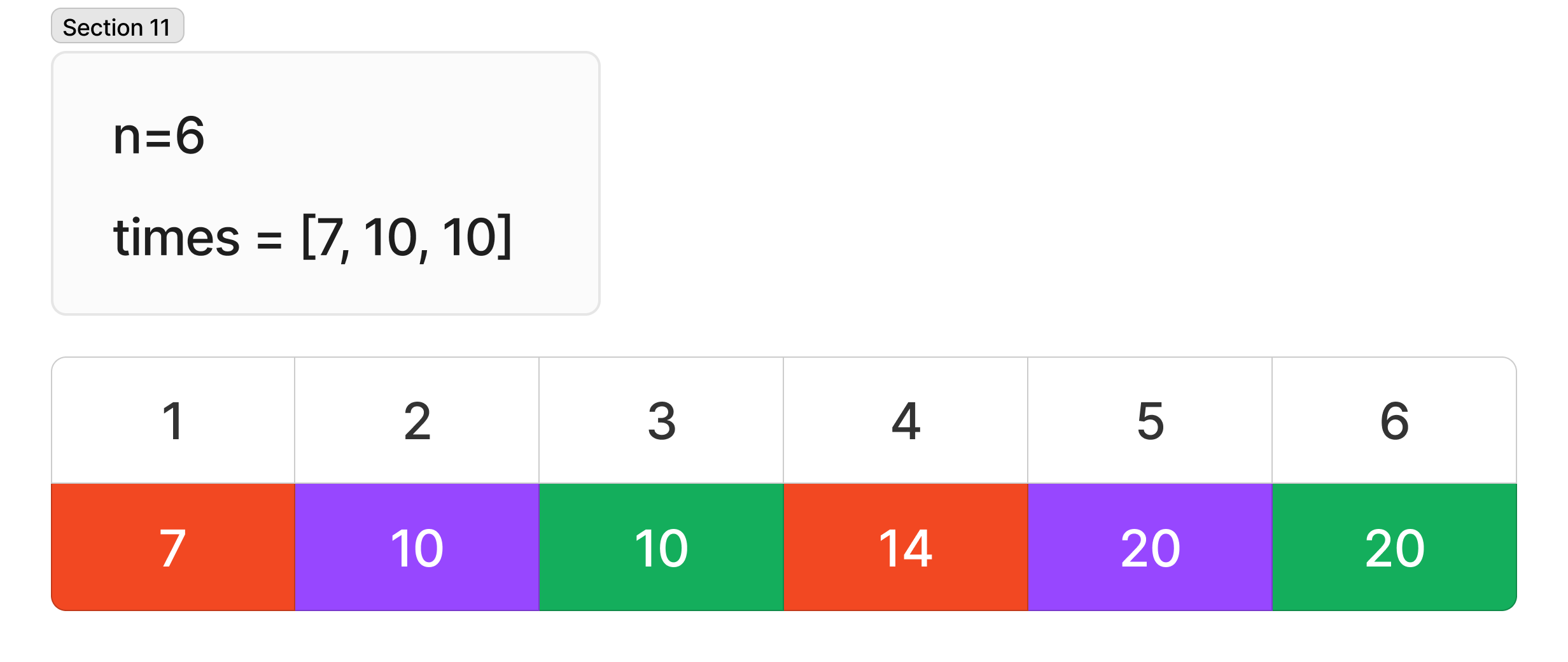
n 이 6 이면서 times 가 [2, 3] 경우는 아래와 같이 8분이 소요된다. 이 케이스로 문제 해결 과정을 설명하겠다.
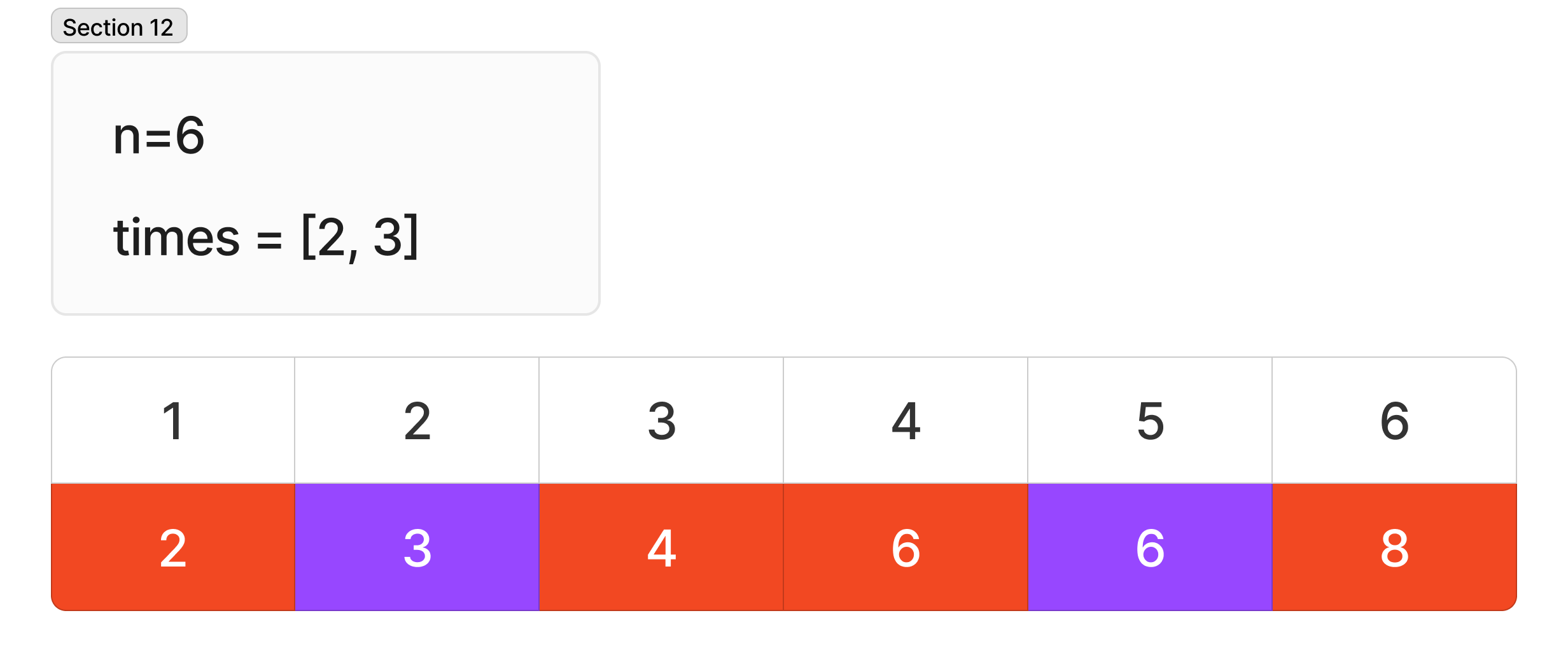
문제 해결 과정
문제를 풀 때 시각화한 것처럼 배열을 만들어서 풀려고하였다. 정답이건 오답이건 시간 초과를 해결할 기미가 보이지 않았다. 제한 사항을 보면 n 의 최대 크기는 1억이다. 즉 비어있는 for 문만 1억 번 돌아도 시간 초과가 발생한다.
알고리즘을 풀 때 자주 느끼는 것은 문제 해결할 때 어떤 값을 관점으로 두고 풀 것이냐가 중요하다고 생각될 때가 많다. 이번 경우에는 이분 탐색인 것은 감이 왔지만 관점을 잘못 두어서 고생을 좀 하였던 것 같다.
이제 문제를 해결 해보자.
아래를 보면 1 ~ 18이 있는데 이 값은 제일 오래 걸리는 심사관의 소요 시간 * n 이다. 즉 최대 시간이다. 다시 말해 제일 오래 걸리는 사람이 모든 사람을 심사하는 경우이다.

심사관 2명은 2, 3 분 씩 걸리기에 시간 별로 처리할 수 있는 사람 수를 아래와 같이 구할 수 있다. 그 값을 다 더하면 각 시간에 몇 명을 처리할 수 있는지 알 수 있다.

우리는 6명을 처리할 수 있을 때의 시간을 구하고 싶다.

시간을 1부터 증가시켜 값을 계산할 수는 없기 때문에 이럴 때 이분 탐색을 통해 효율적으로 값을 구할 수 있다.
L = 1, R = 18
M = 9

시간 9의 값은 찾고자 하는 값보다 크므로 R 을 조정한다.
L = 1, R = 8 (M - 1)
M = 4

찾고자 하는 값보다 작으므로 L 을 조정한다.
L = 5 (M + 1), R = 8
M = 6

L = 7 (M + 1), R = 8
M = 7

마지막으로 L 을 조정하면 6명을 처리할 수 있는 최소 시간이 나온다.
L = 8 (M + 1), R = 8
M = 8

전체 코드
def solution(n, times):
left = 1
right = max(times) * n
answer = right
while left <= right:
mid = (left + right) // 2
if sum(mid // time for time in times) >= n:
answer = mid
right = mid - 1
else:
left = mid + 1
return answer
print(solution(6, [7, 10, 10]), 20)
print(solution(6, [2, 3]), 8)
print(solution(6, [7, 10]), 28)

