요격 시스템
문제 설명
A 나라가 B 나라를 침공하였습니다. B 나라의 대부분의 전략 자원은 아이기스 군사 기지에 집중되어 있기 때문에 A 나라는 B 나라의 아이기스 군사 기지에 융단폭격을 가했습니다. A 나라의 공격에 대항하여 아이기스 군사 기지에서는 무수히 쏟아지는 폭격 미사일들을 요격하려고 합니다. 이곳에는 백발백중을 자랑하는 요격 시스템이 있지만 운용 비용이 상당하기 때문에 미사일을 최소로 사용해서 모든 폭격 미사일을 요격하려 합니다. A 나라와 B 나라가 싸우고 있는 이 세계는 2 차원 공간으로 이루어져 있습니다. A 나라가 발사한 폭격 미사일은 x 축에 평행한 직선 형태의 모양이며 개구간을 나타내는 정수 쌍 (s, e) 형태로 표현됩니다. B 나라는 특정 x 좌표에서 y 축에 수평이 되도록 미사일을 발사하며, 발사된 미사일은 해당 x 좌표에 걸쳐있는 모든 폭격 미사일을 관통하여 한 번에 요격할 수 있습니다. 단, 개구간 (s, e)로 표현되는 폭격 미사일은 s와 e에서 발사하는 요격 미사일로는 요격할 수 없습니다. 요격 미사일은 실수인 x 좌표에서도 발사할 수 있습니다. 각 폭격 미사일의 x 좌표 범위 목록 targets이 매개변수로 주어질 때, 모든 폭격 미사일을 요격하기 위해 필요한 요격 미사일 수의 최솟값을 return 하도록 solution 함수를 완성해 주세요.
시각화
아래와 같이 3번 요격 미사일을 발사하면 모든 폭격 미사일을 요격할 수 있다.
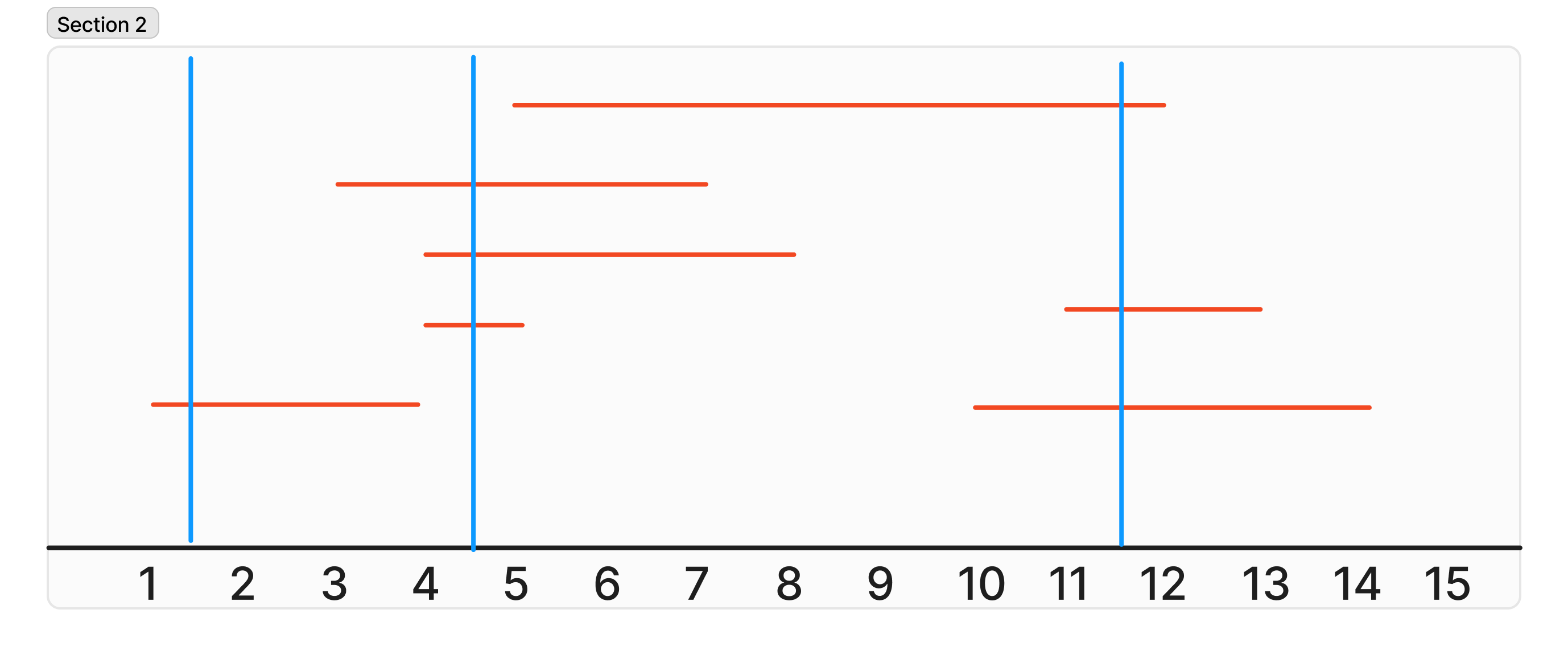
각각 요격 미사일일 때 요격하는 미사일의 범위는 아래와 같다.

문제 해결 과정
어떻게 최소로 요격 미사일을 발사할 수 있을까?
생각해볼 수 있는 것은 무조건 모든 미사일을 요격해야만한다는 것이다. 즉 눈 앞에 있는 미사일부터 요격해야한다. 눈 앞에 있는 미사일을 요격은 하되 범위가 겹쳐 있는 미사일까지 요격한다면 최소개의 미사일을 발사할 수 있다.
일단 미사일을 정렬해서 차례로 처리해보도록 하자. 아래는 미사일을 정렬한 후 모습이다.
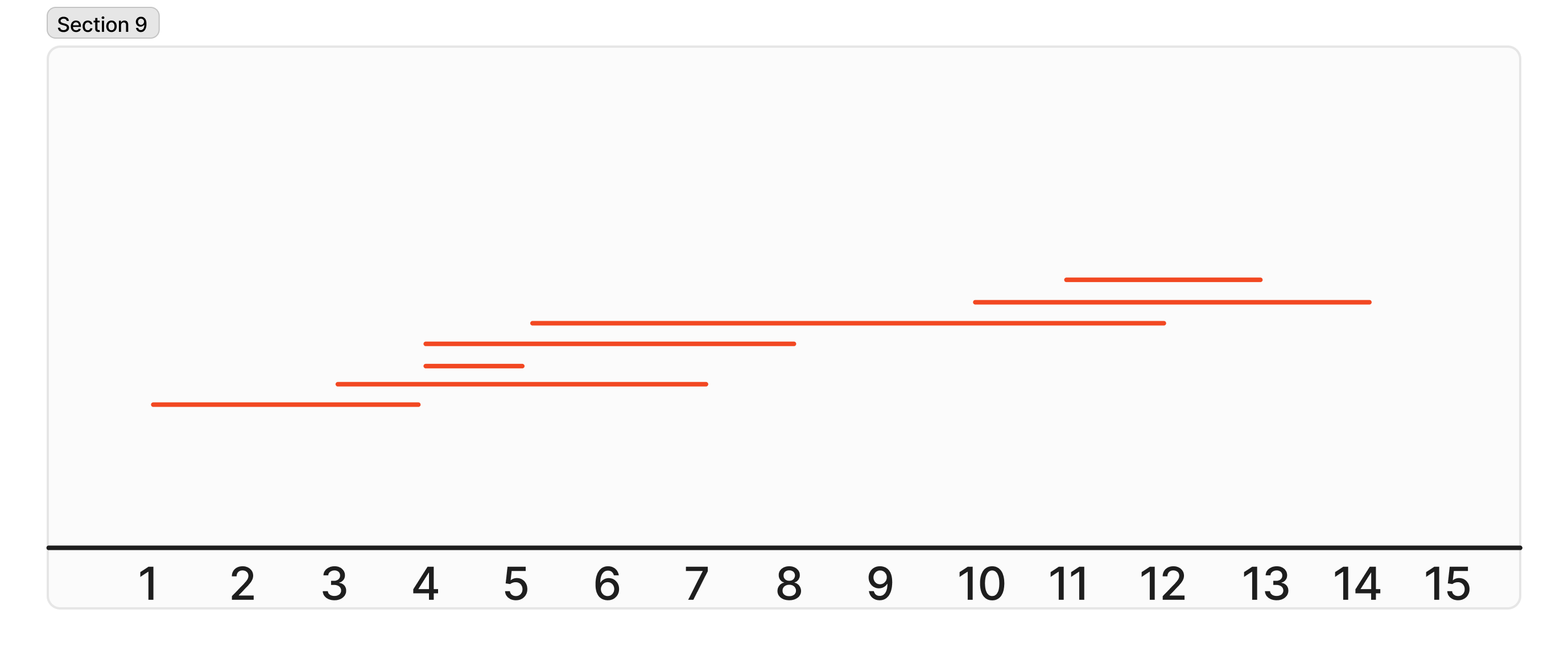
첫 번째 미사일에 범위는 1~4 이기에 4 위치에서 요격 미사일을 발사하면 3 ~ 7의 범위인 미사일도 요격할 수 있게 된다.
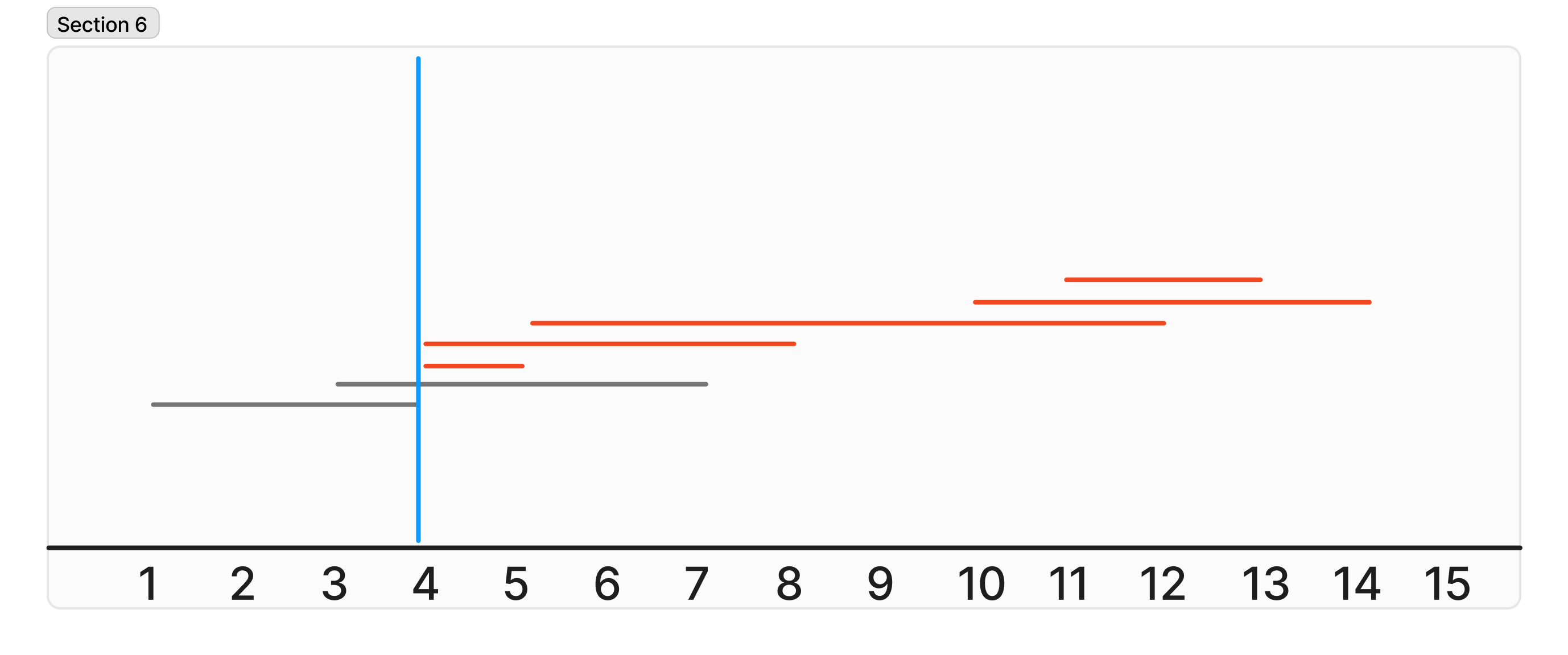
1, 2 미사일이 요격이 되었기에 3번 미사일을 요격해야한다. 3번 미사일은 4 ~ 5 이기에 5 위치에서 요격 미사일을 발사하면 4 ~ 8의 범위인 미사일도 요격할 수 있게 된다.
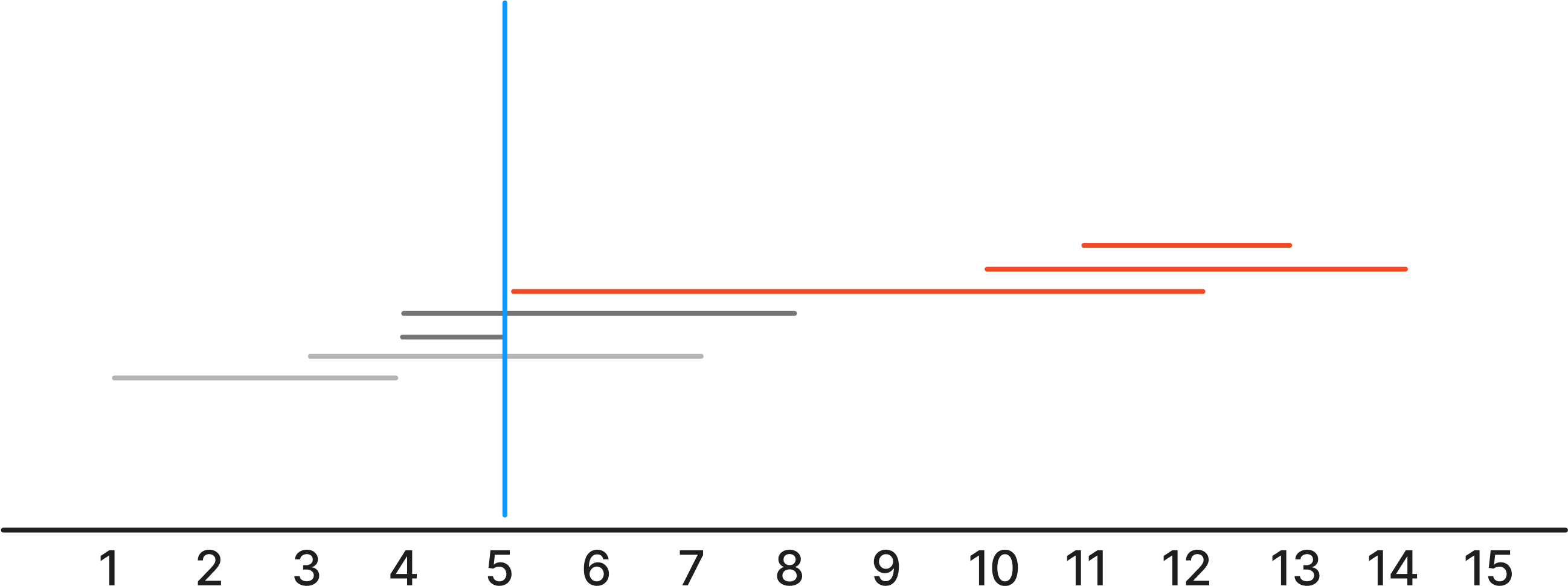
1 ~ 4 미사일이 요격이 되었기에 5번 미사일을 요격해야한다. 5번 미사일은 5 ~ 12 이기에 12 위치에서 요격 미사일을 발사하면 나머지 미사일도 요격할 수 있게 된다.
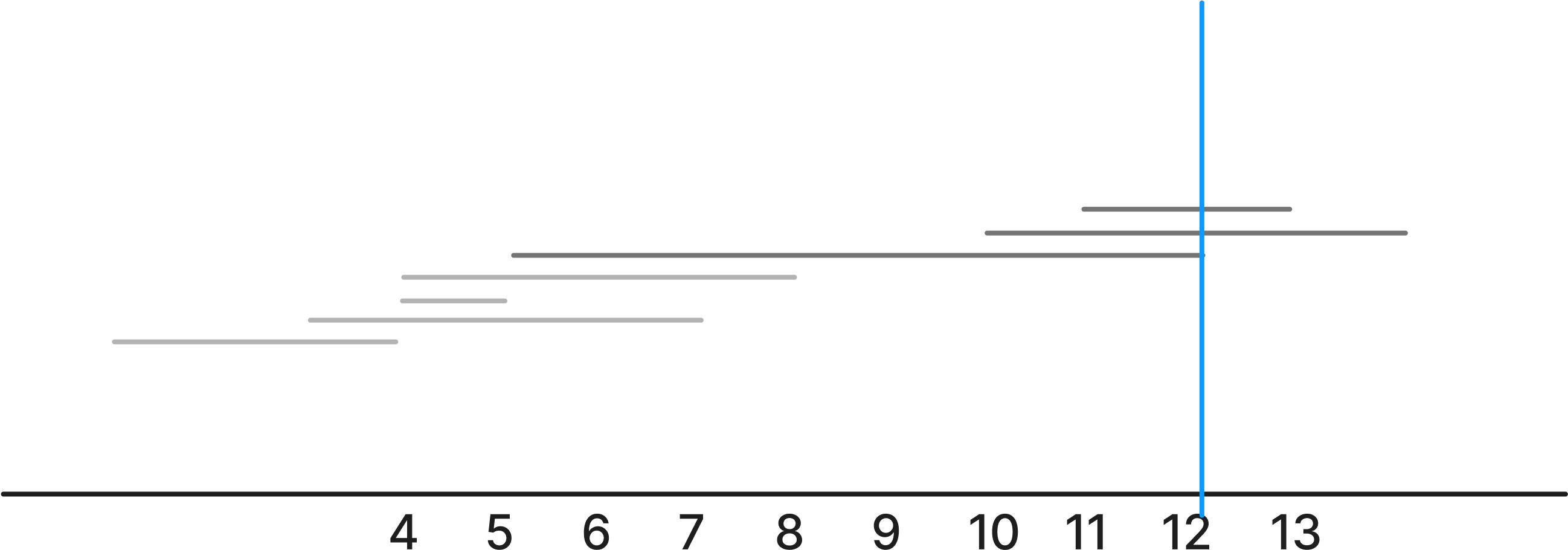
여기서 나름의 규칙을 발견할 수 있다.
- 첫 번째 미사일의 left와 right 범위를 저장합니다.
- 이후 미사일의 범위를 하나씩 확인하며 다음과 같이 처리합니다:
- 만약 현재 미사일의 left가 현재 요격 미사일의 right보다 작거나 같다면,
- 하나의 요격 미사일로 처리할 수 있습니다.
- 요격 범위를 현재 미사일의 right와 현재 요격 미사일의 right 중 더 작은 값으로 갱신합니다.
- 이렇게 하면 다음 미사일도 요격 가능한 최소 범위를 유지할 수 있습니다.
- 만약 현재 미사일의 left가 현재 요격 미사일의 right보다 작거나 같다면,
- 만약 현재 미사일의 left가 현재 요격 미사일의 right보다 크다면,
- 새로운 요격 미사일이 필요합니다.
- 현재 미사일의 범위(left, right)로 새롭게 갱신합니다.
전체 코드
import collections
def solution(targets):
answer = 0
targets.sort(key=lambda x: (x[0], x[1]))
targets = collections.deque(targets)
l, r = targets.popleft()
answer += 1
while targets:
target = targets.popleft()
if l <= target[0] < r:
r = min(target[1], r)
continue
l, r = target
answer += 1
return answer