탐욕법(Greedy) > 섬 연결하기
문제 설명
n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요. 다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.
제한사항
섬의 개수 n은 1 이상 100 이하입니다.
costs의 길이는 ((n-1) * n) / 2이하입니다.
임의의 i에 대해, costs[i][0] 와 costs[i] [1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i] [2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
연결할 수 없는 섬은 주어지지 않습니다.
시각화
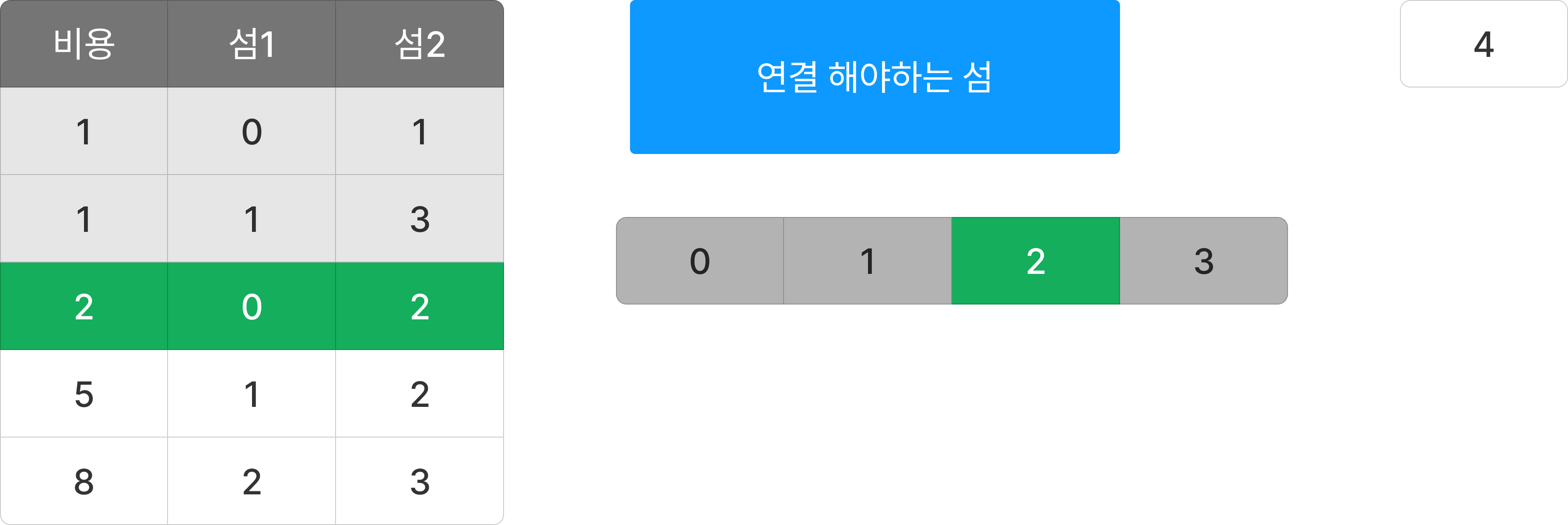
왼쪽과 같이 섬과 비용이 주어졌을 때 오른쪽과 같이 최소 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 구하면 된다.
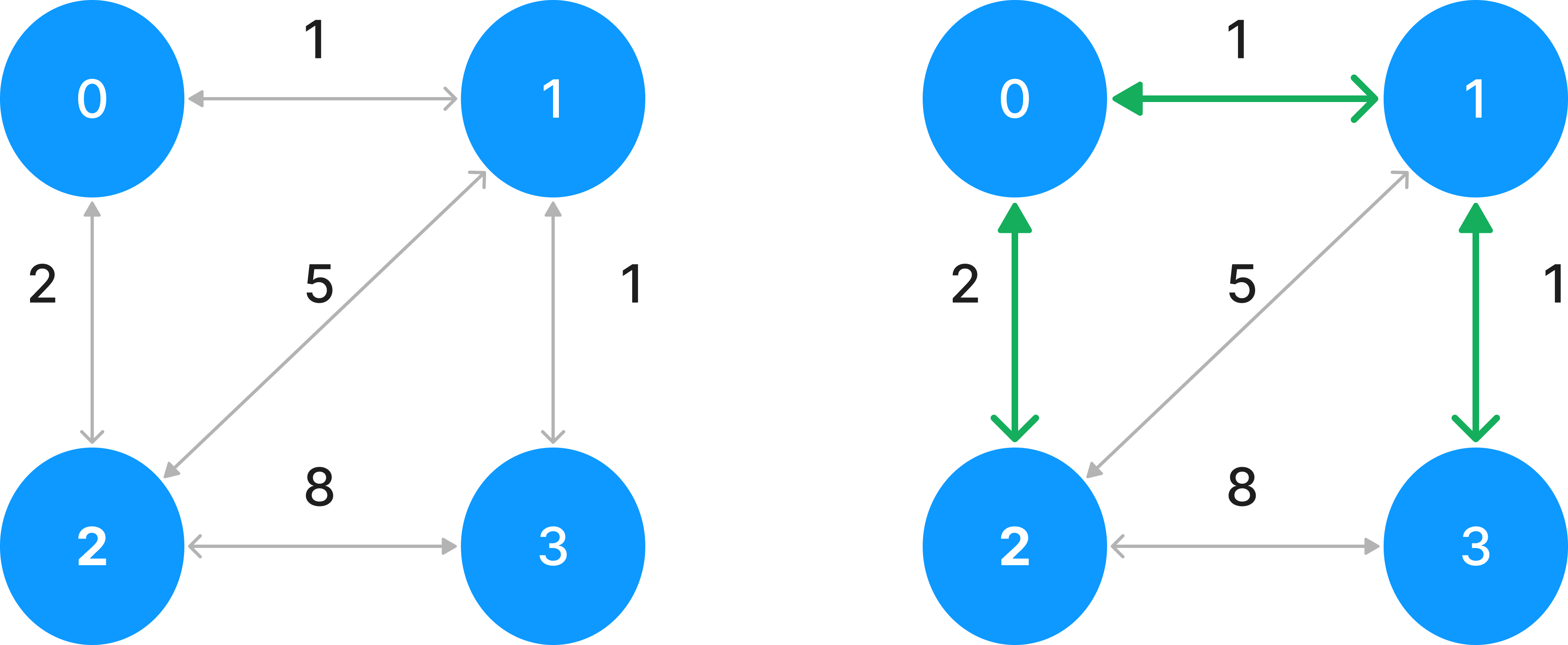
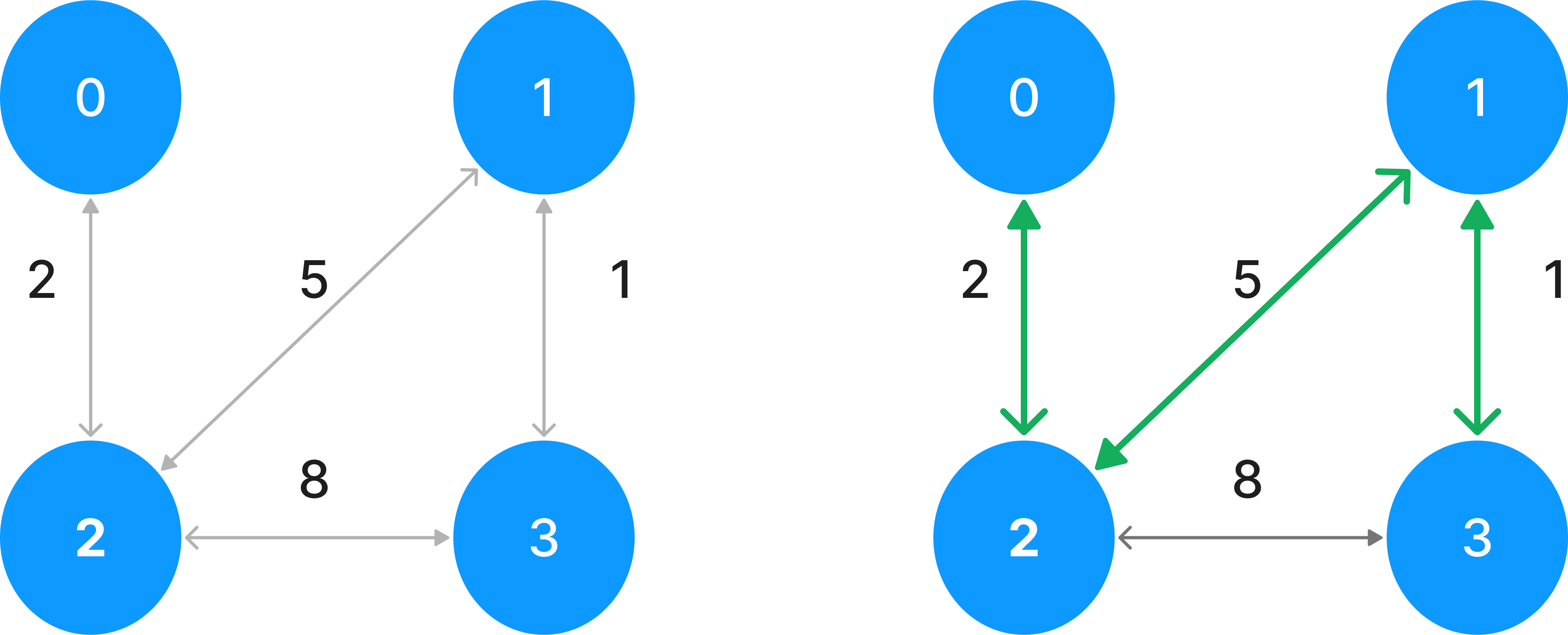
만약 0 과 1을 연결하던 다리를 없앨 경우 아래와 같이 비용이 8로 증가하게 된다.
문제 해결 과정
이 문제는 카테고리에서 나온 것 처럼 그리디 알고리즘 유형이다. 그리디는 간단하게 말하면 현재 상황에서 가장 좋은 것을 선택하는 것이다.
아무래도 탐욕스럽게 선택하는 기준으로는 비용이 될 것이다. 그렇기에 비용을 기준으로 정렬을 해보자.
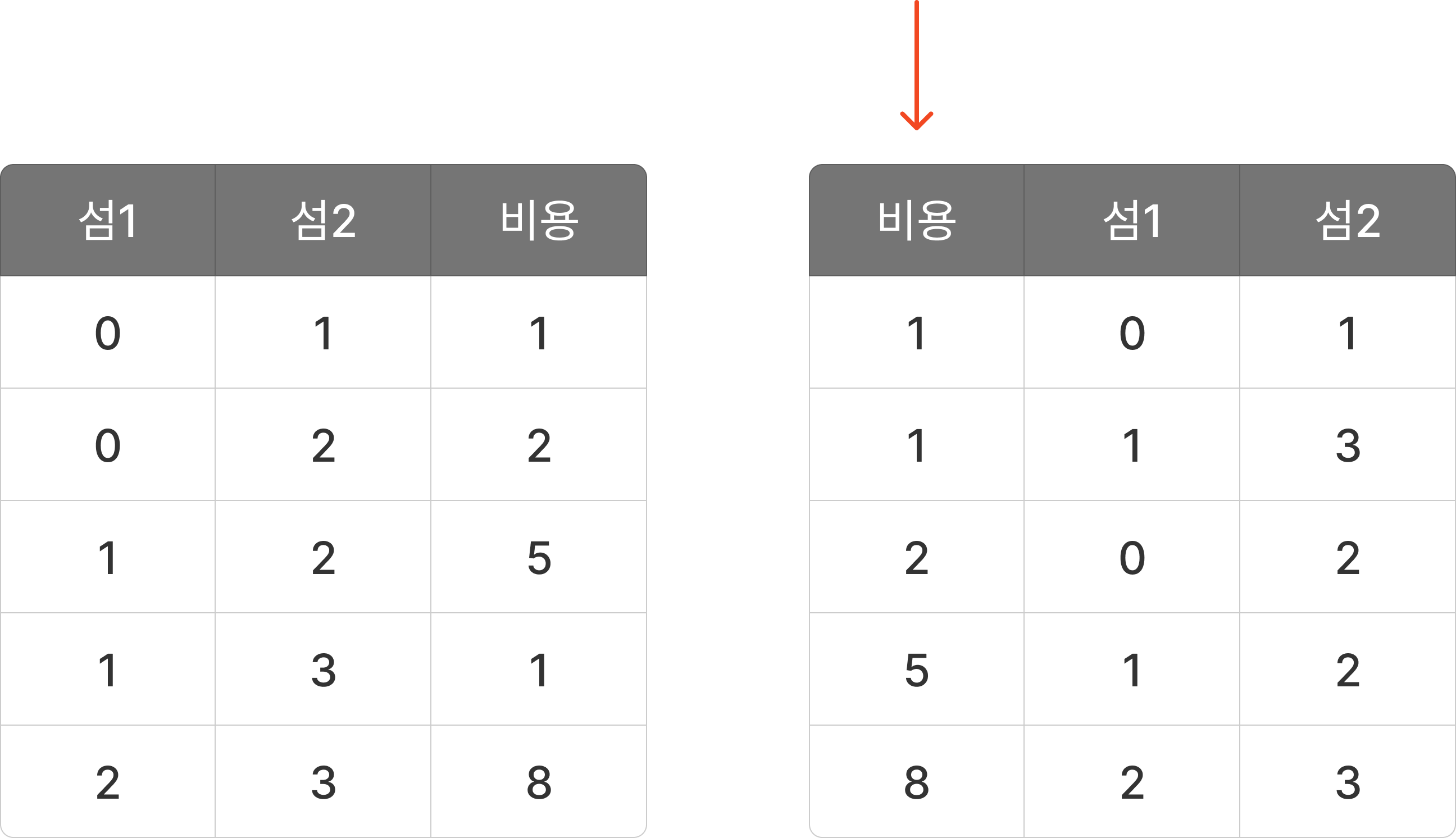
정렬된 섬 정보와 연결 해야하는 섬 리스트를 가지고 최소값을 구해보자.

첫 번째 섬을 선택하고 연결할 수 있는 섬을 연결한다. 그리고 비용을 더해서 가지고 있는다.

계속해서 반복한다.
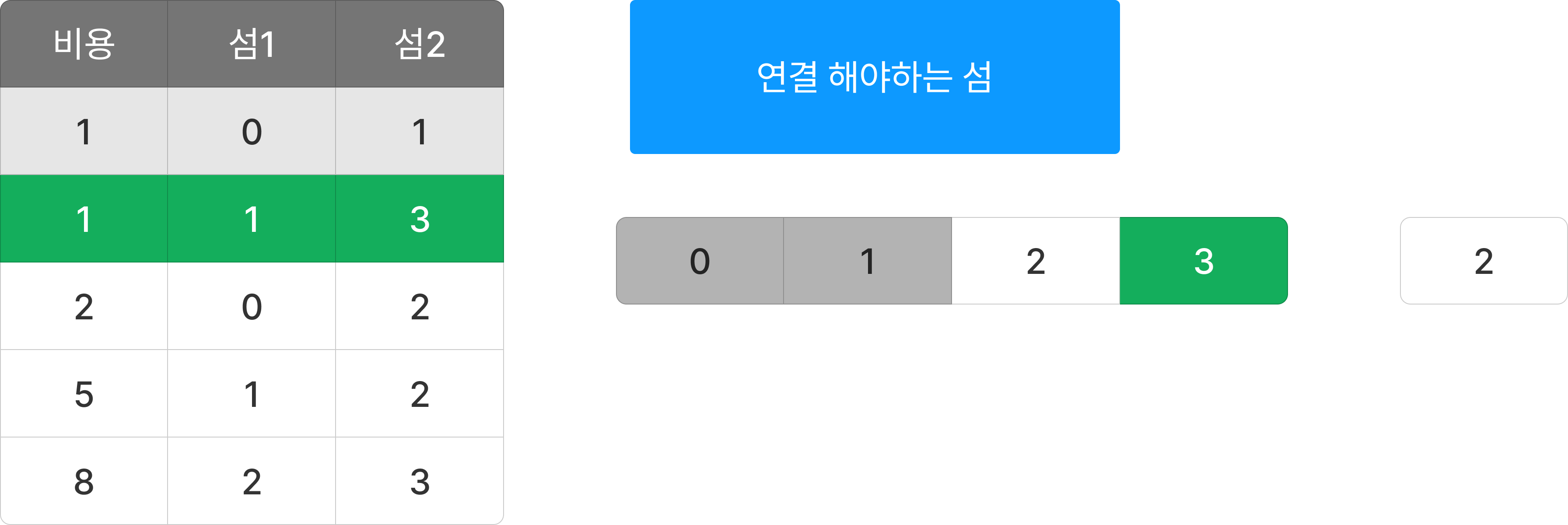
운이 좋게도 이 경에는 3번만에 모든 섬을 연결했다. 모든 섬이 연결이 되면 종료한다.
전체 코드
위 내용을 코드로 구현하면 아래와 같다.
from collections import defaultdict
def solution(n, costs):
answer = 0
island_maps = defaultdict(list)
island_wait_map = [i for i in range(n)]
for cost in costs:
t1, t2, c = cost
island_maps[t1].append((c, t2))
island_maps[t2].append((c, t1))
candidate = island_maps[island_wait_map.pop()]
while island_wait_map:
candidate = sorted(candidate, reverse=True)
c, t2 = candidate.pop()
if t2 not in island_wait_map:
continue
candidate.extend(island_maps[t2])
island_wait_map.remove(t2)
answer += c
return answer
print(solution(4, [[1, 0, 1], [0, 2, 2], [1, 2, 5], [1, 3, 1], [2, 3, 8]]), 4)
print(solution(4, [[0, 1, 1], [0, 2, 2], [1, 2, 5], [1, 3, 1], [2, 3, 8]]), 4)
print(solution(4, [[0, 2, 2], [1, 2, 5], [1, 3, 1], [2, 3, 8]]), 8)

