[PCCP 기출문제] 2번 / 석유 시추
문제 설명
세로길이가 n 가로길이가 m인 격자 모양의 땅 속에서 석유가 발견되었습니다. 석유는 여러 덩어리로 나누어 묻혀있습니다. 당신이 시추관을 수직으로 단 하나만 뚫을 수 있을 때, 가장 많은 석유를 뽑을 수 있는 시추관의 위치를 찾으려고 합니다. 시추관은 열 하나를 관통하는 형태여야 하며, 열과 열 사이에 시추관을 뚫을 수 없습니다.
예를 들어 가로가 8, 세로가 5인 격자 모양의 땅 속에 위 그림처럼 석유가 발견되었다고 가정하겠습니다. 상, 하, 좌, 우로 연결된 석유는 하나의 덩어리이며, 석유 덩어리의 크기는 덩어리에 포함된 칸의 수입니다. 그림에서 석유 덩어리의 크기는 왼쪽부터 8, 7, 2입니다.
시추관은 위 그림처럼 설치한 위치 아래로 끝까지 뻗어나갑니다. 만약 시추관이 석유 덩어리의 일부를 지나면 해당 덩어리에 속한 모든 석유를 뽑을 수 있습니다. 시추관이 뽑을 수 있는 석유량은 시추관이 지나는 석유 덩어리들의 크기를 모두 합한 값입니다. 시추관을 설치한 위치에 따라 뽑을 수 있는 석유량은 다음과 같습니다.
시각화
아래와 같이 석유 맵이 주어진다. 검은색이 석유가 매장 되어있는 것을 의미한다.

매장량을 알기 위해 칸에 index 를 적어보자면 아래와 같다.

석유 시추는 열 기준으로 한 칸 씩 움직이며 석유를 뽑는다. 이 때 석유를 뽑을 수 있는 최대량을 구해야 한다. 첫 번째 열부터 세 번쨰 열까지는 같은 석유 덩어리이다. 즉 어딜 파도 같은 양의 석유를 뽑을 수 있다.
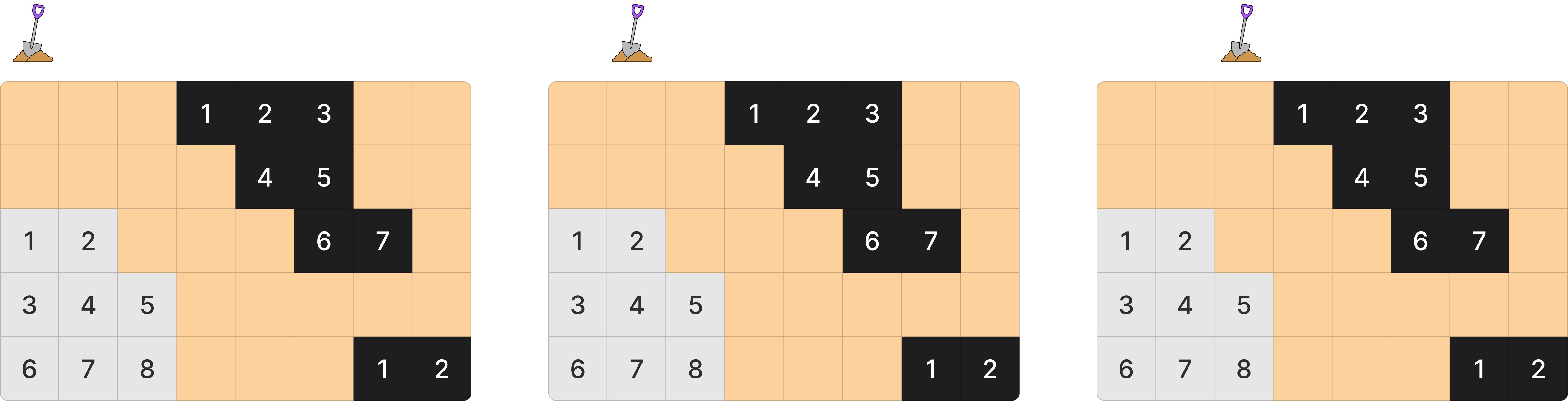
4 ~ 6 열은 다른 석유 덩어리를 파게 된다.
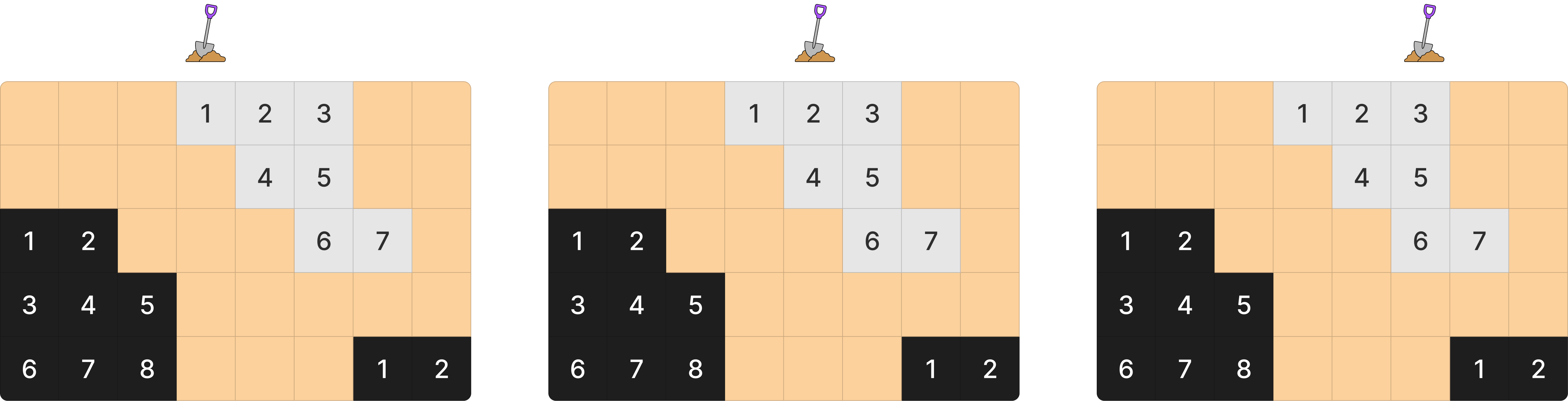
7번 째 열의 경우 두 개의 덩어리를 파게 된다. 즉 7번 째 열을 시추할 경우 9개의 석유를 뽑을 수 있다.
8번 째는 한 개의 덩어리이고 2개의 석유를 뽑을 수 있다.
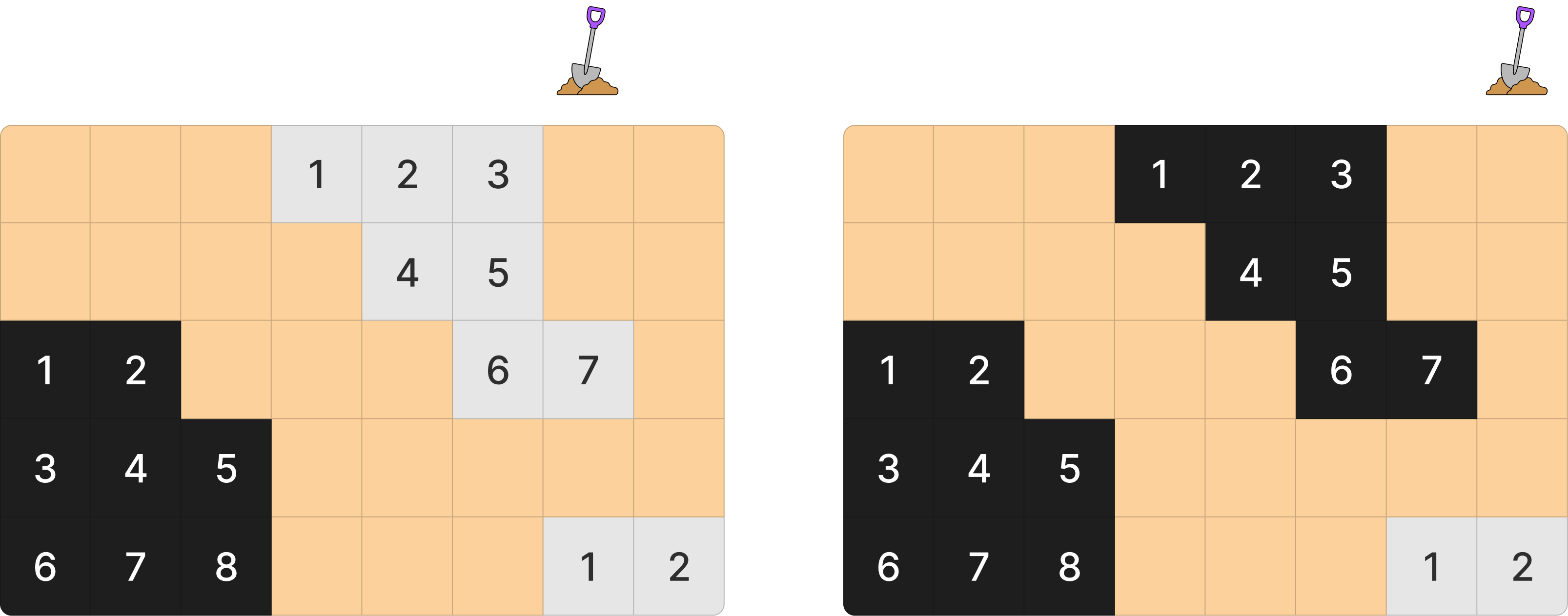
문제 해결 과정
- 석유 덩어리 그룹화
- 각 덩어리에 좌표를 저장
- 각 덩어리에서 column 별로 석유량을 계산
지도를 돌며 석유 덩어리가 발견이 되면 bfs 로 석유 덩어리를 찾아낸다. bfs 를 돌며 반복되지 않도록 해당 좌표를 0으로 바꾸며 석유 덩어리를 찾아낸다.
column 별로 석유량을 계산하기 위해 dictionary 를 사용한다. 하나의 열이라도 해당이 되면 해당 석유 덩어리 전체를 시추할 수 있기 때문에 해당 열의 석유량을 더해준다.
전체 코드
from collections import deque, defaultdict
def solution(land):
def bfs(start_y, start_x):
queue = deque([(start_y, start_x)])
coordinates = []
while queue:
y, x = queue.popleft()
if y < 0 or y >= len(land) or x < 0 or x >= len(land[0]) or land[y][x] == 0:
continue
coordinates.append((y, x))
land[y][x] = 0
for dy, dx in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
queue.append((y + dy, x + dx))
return coordinates
oil_maps = []
for y in range(len(land)):
for x in range(len(land[0])):
if land[y][x] == 1:
oil_maps.append(bfs(y, x))
oil_amount_by_col = defaultdict(int)
for oil_map in oil_maps:
for col in set(coord[1] for coord in oil_map):
oil_amount_by_col[col] += len(oil_map)
return max(oil_amount_by_col.values())
print(solution([[0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 1, 1, 0, 0], [1, 1, 0, 0, 0, 1, 1, 0], [1, 1, 1, 0, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 0, 1, 1]]), 9)
print(solution([[1, 0, 1, 0, 1, 1], [1, 0, 1, 0, 0, 0], [1, 0, 1, 0, 0, 1], [1, 0, 0, 1, 0, 0], [1, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1]]
), 16)