도넛과 막대 그래프
2024 카카오 윈터 인턴쉽 문제가 오픈되어 풀어보았다.

문제 설명
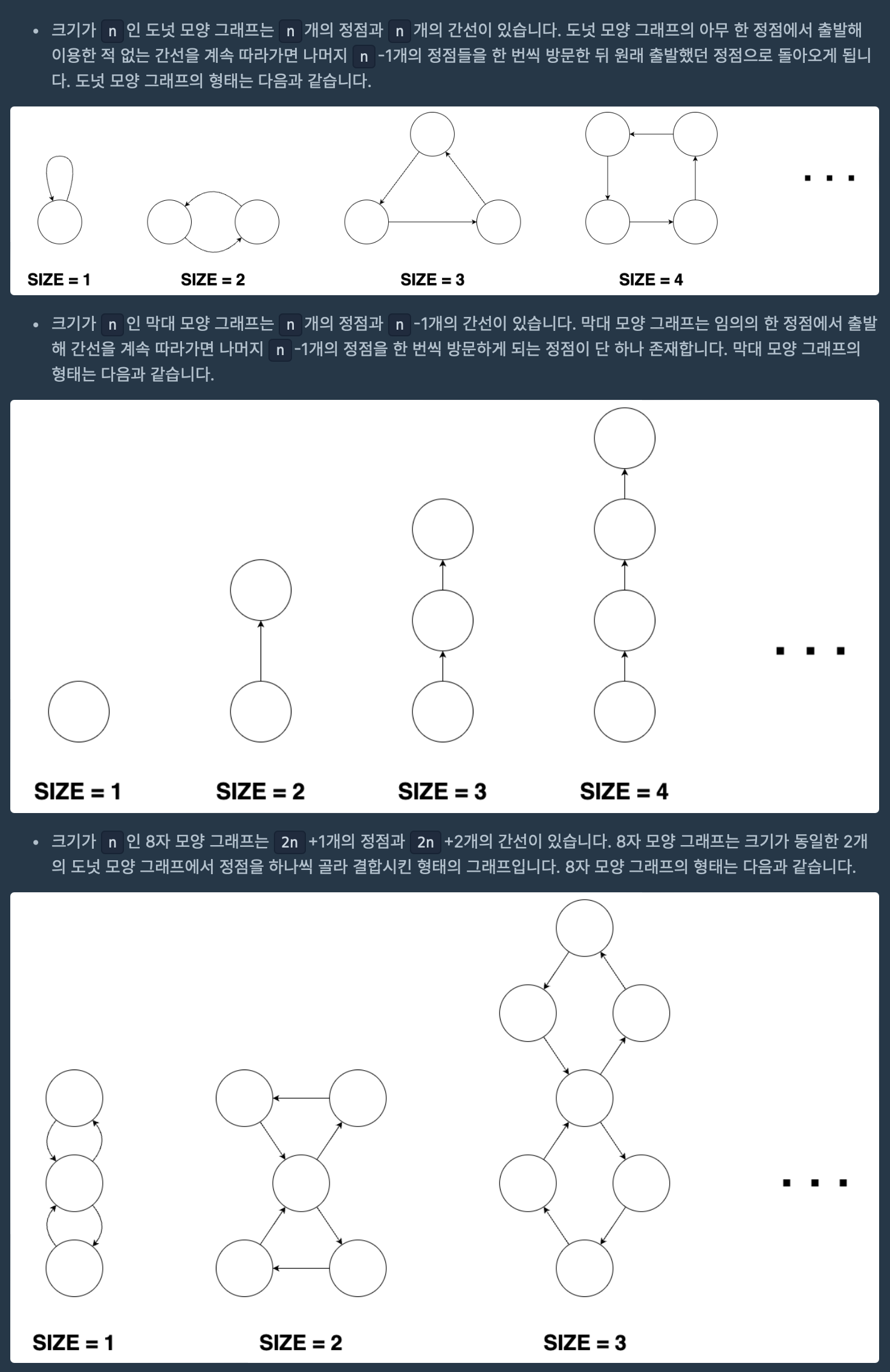
- 그래프가 있는데 그래프의 모양이 도넛과 막대로 이루어져있다.
- 그래프가 여러개 있는데 각 그래프를 연결하는 임의의 정점이 하나가 있다.
임의의 정점과 그래프 종류 개수를 반환해라
흐름 파악
흐름 파악을 위해 꼬리에 꼬리를 무는 방식으로 접근하려한다.
임의의 정점은 어떻게 구할 수 있을까?
임의의 정점은 각 그래프를 연결하기에 간선이 제일 많은 노드가 임의의 정점이다.
그러나 그래프에서 한 노드가 2개의 노드를 가리킬 수 있지만 3개는 가능하지 않기 때문에 조건문도 추가하여 이른 리턴을 하게되면 속도에 도움이 될 것이다.
임의의 정점과 연결된 부분이 그래프의 첫 노드가 아니여도 괜찮을까?
도넛의 경우 간선을 타고 진행하다보면 자신이 나오기에 문제가 없다.
막대의 경우 간선을 타고 진행하다보면 끝이 결국 있이게 문제가 없다.
8자 그래프의 경우도 도넛과 마찬가지로 간선을 타고 진행하다보면 자신이 나오기에 문제가 없다.
그래프 종류는 어떻게 구할 수 있을까?
도넛, 막대, 8자 그래프의 특징을 파악해보자.
도넛
간선을 타고 노드를 탐색하면 처음 노드가 나온다
막대
간선을 타고 노드를 탐색하면 다음 노드가 없다
8자 그래프
간선을 타고 노드를 탐색하다보면 다음으로 갈 수 있는 간선이 2개가 나온다.
8자 그래프의 경우 간선이 2개 나올 경우 이른 리턴을 하면 된다.
from collections import defaultdict
def solution(edges):
answer = []
graph_8_count = 0
graph_bar_count = 0
graph_donut_count = 0
def find_center_node():
start_a_dict = defaultdict(int)
m_k, m_v = 0, 0
for edge in edges:
start_a_dict[edge[0]] += 1
if start_a_dict[edge[0]] > m_v:
m_k = edge[0]
m_v = start_a_dict[edge[0]]
if m_v == 3:
return m_k
return m_k
center_node = find_center_node()
def remove_and_get_start_nodes_start_center_node():
start_nodes = []
for edge in edges:
if edge[0] == center_node:
start_nodes.append(edge[1])
return start_nodes
start_nodes = remove_and_get_start_nodes_start_center_node()
edge_dict = defaultdict(list)
for edge in edges:
if edge[0] == center_node:
continue
edge_dict[edge[0]].append(edge[1])
for start_node in start_nodes:
groups = [start_node]
is_graph_8 = False
r = start_node
while r in edge_dict:
r_dest_nodes = edge_dict[r]
if len(r_dest_nodes) > 1:
is_graph_8 = True
break
r = r_dest_nodes[0]
groups.append(r)
if r == start_node:
break
if is_graph_8:
graph_8_count += 1
elif len(groups) == 1:
graph_bar_count += 1
elif groups[0] == groups[-1]:
graph_donut_count += 1
else:
graph_bar_count += 1
return [center_node, graph_donut_count, graph_bar_count, graph_8_count]
print((solution([[2, 3], [4, 3], [1, 1], [2, 1]])), [2, 1, 1, 0])
print((solution(
[[4, 11], [1, 12], [8, 3], [12, 7], [4, 2], [7, 11], [4, 8], [9, 6], [10, 11], [6, 10], [3, 5], [11, 1], [5, 3],
[11, 9], [3, 8]])), [4, 0, 1, 2])
print((solution(
[[4, 11], [1, 12], [8, 3], [12, 7], [4, 2], [7, 11], [4, 8], [9, 6], [10, 11], [6, 10], [3, 5], [11, 1], [5, 3],
[11, 9], [3, 8], [20, 20], [4, 20]])), [4, 1, 1, 2])
